第10回 凝集速度・半減期と安定度比
DLVO理論ではコロイド粒子の凝集は不可逆過程とみなし、次の2つの過程からなると考える。①2つの粒子(1次粒子)が熱運動(ブラウン運動)をしながら互いに接近する拡散過程。②接近後、互いに不可逆的に付着して、2個の1次粒子が消滅し1個の2次粒子が生成する過程。両過程とも粒子間相互作用に依存する。
①の過程では、2つの粒子は互いに力を及ぼしあいながら、その力のポテンシャル場の中で運動する。粒子同士の接近は粒子間の引力が強ければ促進され、粒子間の斥力が強ければ妨げられる。②の過程では、2つの粒子の接近から付着に至るには、粒子間相互作用のポテンシャル障壁Vmaxを超える必要がある。粒子間の斥力が強くVmaxが高ければ2つの粒子の付着は起こりにくく凝集は妨げられ、引力が強くVmaxが低い場合は容易に凝集が起こる。第8回では分散系安定性評価の指標として過程②のみ考えた。今回は①と②の両過程を考慮し、凝集の半減期(凝集速度に反比例)と安定度比を用いて議論する。
粒子間に力が働かない場合(自由拡散)、初期粒子濃度がC0 (m-3) である分散系の粒子濃度がC0/2まで半減する時間(半減期)T1/2はT1/2 = 3η/4kTC0 (秒)で与えられる(Smoluchowski)。この式から以下のことがわかる。(i) 粒子濃度が高いほど2粒子の衝突頻度が上がり半減期T1/2は短くなる。(ii) 温度が高いほど粒子のブラウン運動が盛んになりT1/2は短くなる。(iii) 媒質の粘度ηが高いほど、粒子の運動が抑えられT1/2は長くなる。水中(室温)でC0 = 2×1015 m-3の場合、T1/2 = 80秒となり、Zuorilaの実測値(金ゾル)とよく一致する。
DLVO理論による粒子間相互作用V(H)を考慮すると(粒子の表面電位ψo、粒子半径a、表面間距離H、媒質は価数zの対称型電解質溶液。第8回(1)式参照)、半減期は変化する。粒子が帯電していない場合、粒子間にvan der Waals引力が働くため自由拡散の場合より半減期T1/2は短くなる。粒子が帯電してポテンシャルの山Vmaxが高くなると、T1/2は長くなり分散系は安定に向かう。安定度比Wは粒子が帯電することによってT1/2が長くなる(凝集速度が遅くなる)度合いを表す。すなわち、W = 半減期(帯電)/半減期(非帯電) = 凝集速度(非帯電)/凝集速度(帯電)で与えられ、W = q/qoで定義される。ただし
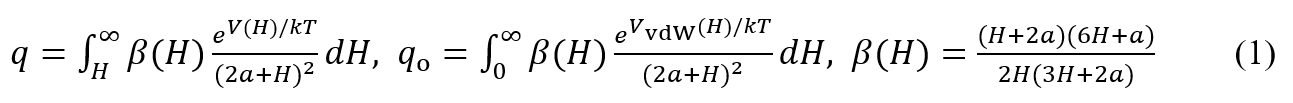
である (McGown-Parfltt)。qoの式に登場するVvdW(H)はvan der Waals相互作用を表すV(H)(第8回(1)式)の第2項である。また、β(H)はHonig–Roebersen–Wiersemaによる流体相互作用補正項である。単独の粒子の拡散定数と距離Hに他の粒子が存在する場合の拡散定数は異なり、1/β(H)に減少するので、補正が必要になる。
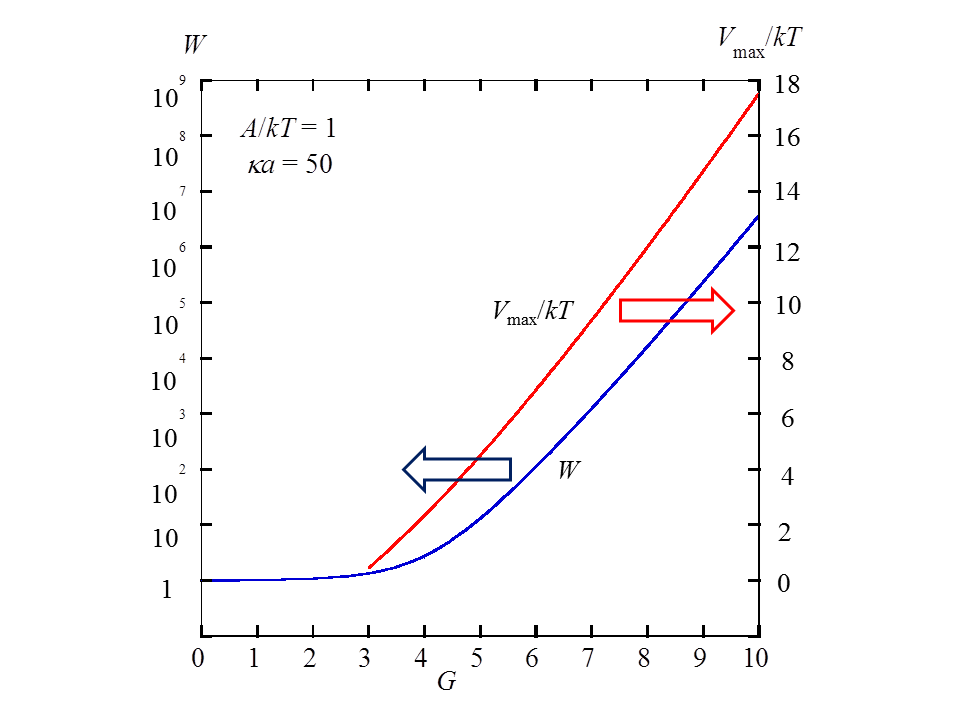
図1 WとVmax/kTのG依存. A/kT =1, κa =50
安定度比Wが大きいほど、系の安定性は増す。図1に安定度比Wおよびポテンシャルの山Vmaxの計算例を示す(A/kT =1, κa =50の場合)。WとVmaxをGの関数として与えてある。 ただし、G = 384πγ2εrεokT/z2e2κおよびγ = tanh(zeψo/kT)である(第8回参照)。表面電位ψoを上げると、Wが劇的に増大することがわかる。なお、 (1)式は数値積分を含むが、Wに対して数値積分を含まない高精度の近似表現も導かれている(第8回文献1)。

