第5回 帯電表面のみかけの表面電位
電解質水溶液中における平面状帯電表面(表面電位ψo)周囲の電位分布ψ(x)を求めよう。表面に原点x=0をとり、表面に垂直に電解質溶液中に向かってx軸を定める。簡単のために、電解質は価数z 、バルク数密度n (m-3)の対称型とする。場所xにおける電位ψ(x)は以下のPoisson-Boltzmann方程式に従う。
 (1)
(1)ψ(0) =ψoおよびψ(∞) = 0を満たす(1)式の解は次式で与えられる。
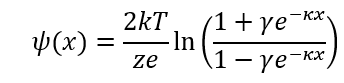 (2)
(2)
ここで、γ = tanh(zeψo/4kT)およびκはDebye-Hückelのパラメタである。 (1)式をψ(x)に関して線形化すると、Debye-Hückel方程式 d2ψ/dx2 =κ2ψが得られる。
Debye-Hückel方程式の解はψ(x)=ψoe-κxである。この解の精度は線形化から予想されるよりはるかに良く、1:1電解質(z=1)の場合、ψo=50mV程度まで適用できる。(2)式はxの大きい所では、ψ(x)=(4kT/ze)γ-κxに漸近する(図1の実線と点線がx ≥1/κでほぼ一致する)。これは、粒子を遠くから眺めたときの見かけの表面電位(有効表面電位)ψeffが(4kT/ze)γになることを意味する。図1と図2に電位ψ(x)の計算例(ψo=50mVおよび150mV))およびψeffとψoの関係を与えた。
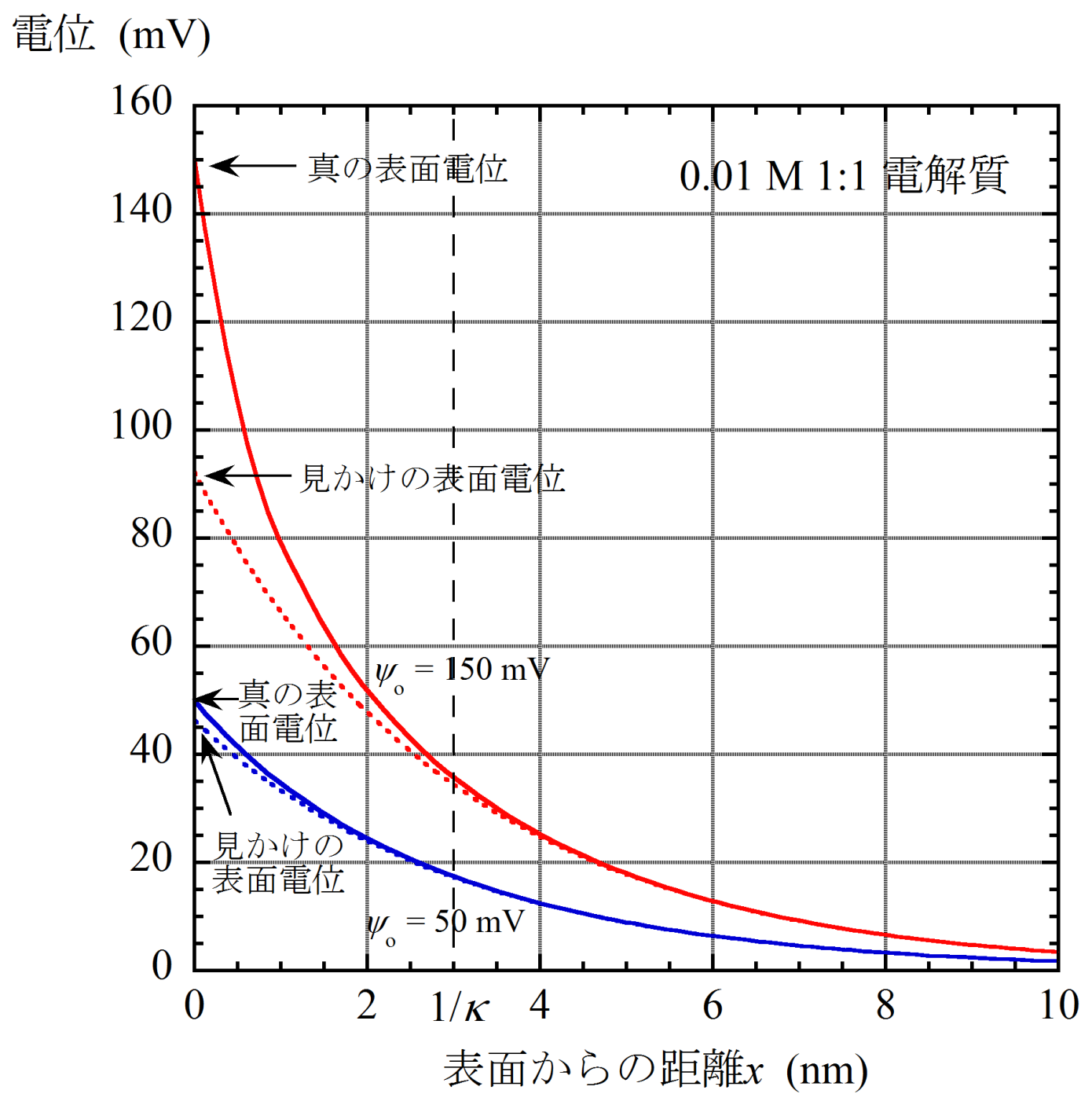
図1 平面状帯電表面近傍の電位分布25℃0.01M1:1電解質水溶液中.
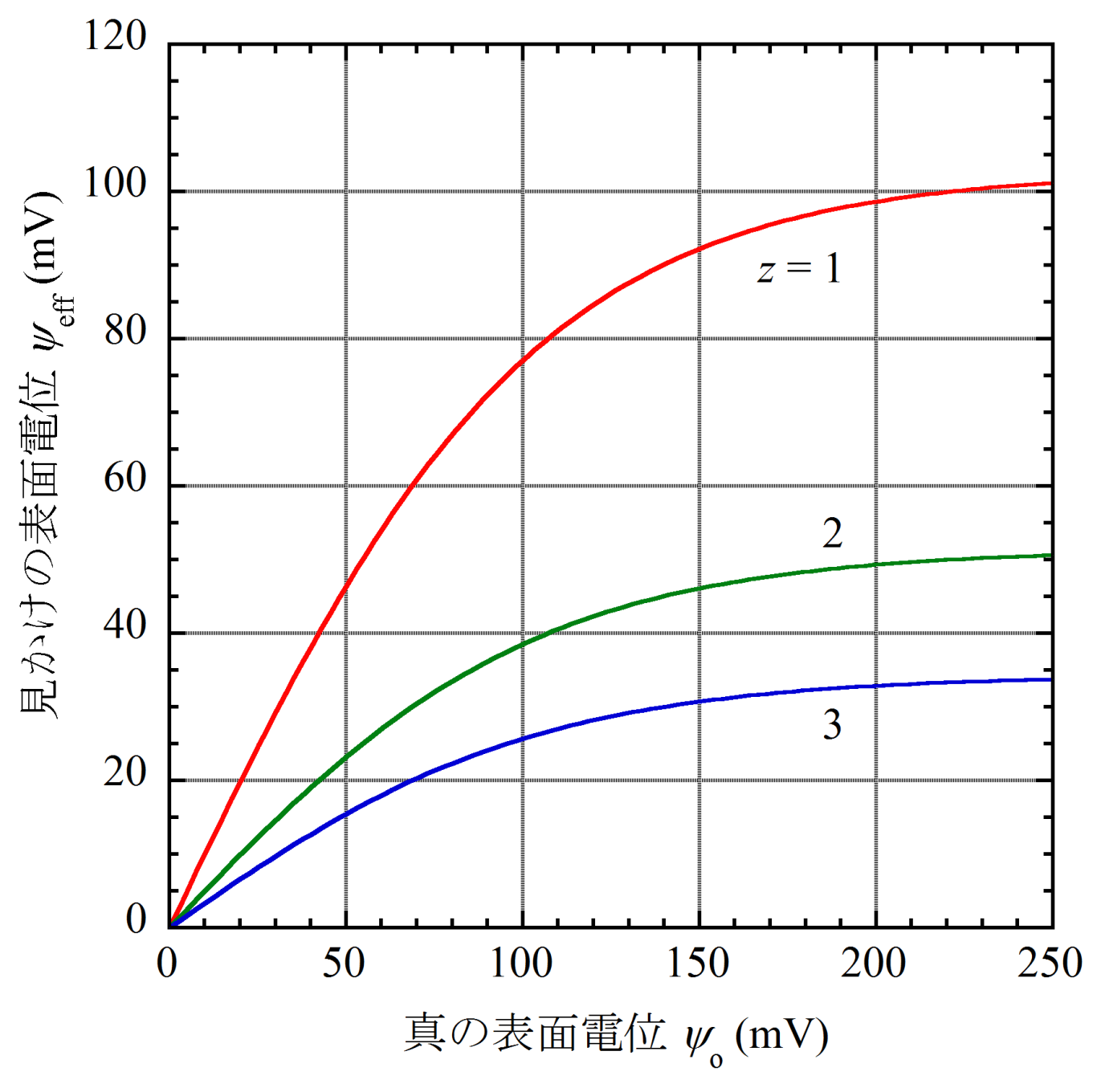
図2 平面状帯電表面の表面電位と
見かけの表面電位(有効表面電位)25℃. z = 1, 2, 3.
表面電位ψoが低い場合、ψeffとψoの差は小さく(図1)、ψeffはψoの増加とともに増加するが、やがて頭打ちになる。この最大の有効表面電位は、1:1型電解質 (z=1) 中の表面では、102.8mV、2:2型 (z=2)では51.4mV、3:3型 (z=3)では、34.3mVである。次回以降で詳述するが、コロイド粒子の分散安定性を決定するのは、真の表面電位ψoではなく、見かけの表面電位ψeffである。

