第16回 気体:コロイド分散系の一つのモデル
自然は2つの意思をもっている。(1)「確率の大きい状態へ」と(2)「力に逆わない」である。コロイド粒子の分散系では、一般に液体媒質中にあって、コロイド粒子間にvan der Waals引力と拡散電気二重層の重なりに起因する静電斥力が働く。もし、これらの力が存在しないと仮定すると、真空中の理想気体の挙動と本質的に同じである。理想気体は互いに力を及ぼさない分子の集団であり、その挙動は(1)の「確率の大きい方へ」という意思のみで決定される。
静止した容器中にある理想気体を考えよう。容器は静止しているが、分子は静止しているわけではなく、無秩序・不規則な運動すなわち熱運動を行っている。コロイド分散系でも同じである。粒子は無秩序・不規則な熱運動を行っている。コロイド粒子の熱運動はとくにブラウン運動とよばれる。分子が単原子分子である場合、1個の分子のもつ平均運動エネルギーはE = (3/2)kTである(ただし、k = Boltzmann定数、T = 絶対温度)。n個の分子では、総エネルギーはE = (3/2)nkTになる。コロイド粒子の場合も同じように、平均の運動エネルギーは E = (3/2)kTで与えられる。
理想気体の重要な性質は真空中への膨張である。はじめ、容器(体積V)の中の小部分(体積v)にn個の理想気体分子が仕切りで閉じ込められているものとする。外部との間に熱の出入りのない条件(断熱条件)のもとで、仕切りを取り去ると分子集団は容器全体に広がる(図1)。これは元の状態には戻らない不可逆過程である。理想気体の断熱自由膨張とよばれる。ここで、理想気体なので分子間には引力も斥力も働いていない。分子集団は分子間斥力で拡がったのではなく、(1)の「確率の大きい状態へ」という自然の意思で拡がったのである。仕切りを取り去った後に1個の分子が小部分に存在する確率はvに比例し、全体に拡がる確率は全体積Vに比例する。n個の分子すべてが小部分に存在する確率はvnに比例し、全体に拡がる確率はVnに比例する。Vnはvnに比べて圧倒的に大きい。こうして、理想気体は「確率の大きい状態へ」という自然界の意思にしたがって、容器全体に拡がる。
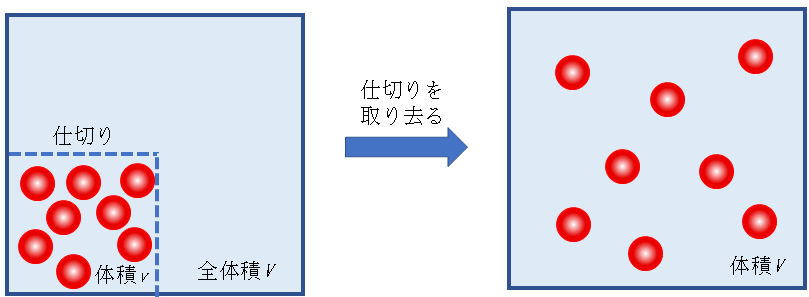
図1 理想気体の断熱自由膨張
n個の分子の確率は1個の確率のn倍ではなくn乗になる。すなわち、分子全体の確率が個々の分子の確率の和ではなく積で与えられる。一方、分子集団のエネルギーは個々のエネルギーの和で与えられる。そこで、Boltzmannは確率の代わりにその対数をとれば、積が和に変換され、エネルギーと同じように扱うことができる。しかも対数をとっても大小関係は変わらず、確率が大きいとその対数も大きい。こうして、確率の代わりに、1個の分子のエントロピーS = k lnV + 定数が導入された(ここで、k = Boltzmann定数)。n個の分子全体のエントロピーはS = k ln Vn = nk ln V+定数になる。断熱自由膨張は、熱が入ってこないのにエントロピーが増加する過程であるから不可逆過程である。
次回のコラムで力の代わりにポテンシャルエネルギー(力に逆らっている度合い)が導入される。ベクトルである力よりもスカラーであるポテンシャルエネルギーの方が使いやすいからある。こうして、自然のもつ2つの意思は(1)「エントロピーの大きい方へ」と(2)「ポテンシャルエネルギーの低い方へ」のように言い換えられる。

