第6回 拡散電気二重層の重なりによる2粒子間の静電反発エネルギー
電解質水溶液中において2個の帯電粒子が接近すると、それぞれの粒子周囲の電気二重層が重なる。この結果、2粒子の間の部分における対イオンの濃度が上昇し、対イオンの浸透圧が増大するため、粒子間に静電斥力が生じる。これが、コロイド粒子の分散安定性の基礎理論であるDerjaguin-Landau-Verwey-Overbeek (DLVO) 理論の重要な結論である。図1に互いに接近する2粒子(表面間距離Η、半径α)周囲の対イオンの濃度分布の計算例を示した。2粒子に挟まれた部分の対イオン濃度が上昇していることがわかる。
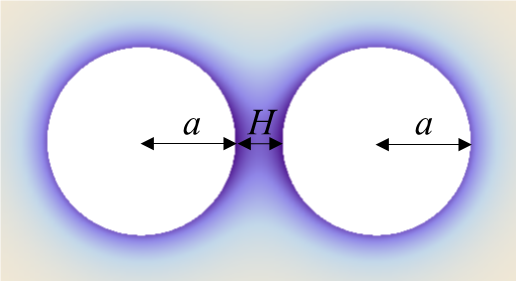
図1 2個の球状粒子(半径α、表面電位25 mV、表面間距離Η) 周囲の対イオン濃度分布.
1/κ = Debye長, κα =2. Η=1/κ. Mathematica DensityPlotによる計算 (濃度の高低を濃淡で表す). 25℃.
価数z、数密度n (m-3) の対称型電解質溶液中にあって距離h離れた2枚の平行な同種平板(表面電位ψo)の場合、平板間の静電斥力P(h)(単位面積当たり)は次式で与えられる。
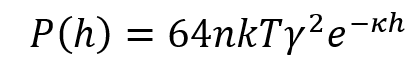 (1)
(1)(1)式は次のようにして求められる。2平板間に挟まれた中央の場所の電位ψmは、一方の平板が距離h/2の場所につくる電位ψ(h/2)の2倍にほぼ等しい(ψm ≈ 2ψ(h/2))。
第5回で述べたPoisson-Boltzmann方程式の解より、ψ(h/2) ≈ ψeffexp(-κh/2)である。ここで、ψeffはψeff = (4kT/ze)γで定義される有効表面電位(見かけの表面電位)である。ただしγ = tanh(zeψo/kT)である。
ψeffを用いて浸透圧を計算した結果が(1)式である。(1)式をhに関して積分すると平板間静電斥力のポテンシャルエネルギーが求まる。さらに、平板間相互作用から2球(半径α、表面間距離Η)の静電反発エネルギーV(H)を求めるには、Derjaguin近似とよばれる便利な近似計算法がある。この近似を用いると、平板間の相互作用エネルギーをhに関してHから∞まで積分し、παを掛けると、2球の相互作用エネルギーが得られる。結果は次式で与えられる。
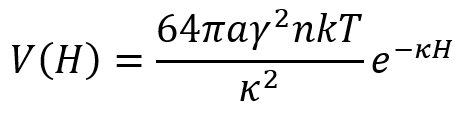 (2)
(2)
ψoが高いとき、γ ≈ 1となりψeffがψoに依存しない一定値4kT/zeに近づく。この結果、ψoを高くしても、表面間距離Hにおける2球間静電相互作用エネルギーV(H)の最大値は64παnkTe-κH/κ2で、この値を超えることはなく、V(H)は表面電位に依存しなくなる。
いずれ、詳述するが、この事実はDLVO理論の成功に深く関係している。有機溶媒等の非水系では、粒子周囲の電位分布はクーロン電位で近似できる(第4回参照)。したがって、表面間距離Hにある2球(半径;α)の間の静電反発エネルギーは次式で与えられる。
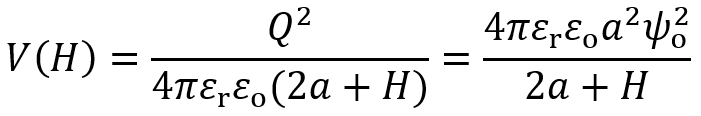 (3)
(3)
