第14回 Hamaker定数のマクロな表現
Hamaker定数は微粒子分散系の凝集促進因子である。第2回コラムではHamakerにしたがって、2個のコロイド粒子1と2の間に働く粒子間引力エネルギーを粒子1と粒子の2のそれぞれを構成する原子(あるいは分子)間van der Waals引力エネルギー-C/r6 (r = 分子間距離、C = London-van der Waals定数) の総和から求めた。分子間van der Waals引力相互作用には、以下の3種類がある。
(1)Keesom相互作用:2個の極性分子間の永久双極子間引力。
(2)Debye相互作用:極性分子と非極性分子間の永久双極子-誘起双極子間引力。
(3)分散相互作用:極性・非極性にかかわらず、分子内に無秩序に量子力学的なゆらぎ双極子が生じる。このゆらぎ双極子間に引力が働く。
以上の3種類(1)〜(3)の相互作用の中で、分散相互作用の寄与が最も大きい。Hamaker理論によれば、真空中における表面間距離hの2枚の平行な同種平板状粒子間のvan der Waals引力エネルギーV(H)はV(H) = -A/12πh2で表される。この式のAがHamaker定数であり、A = C2πN2で与えられる。Nは分子密度である。
さらにC = 3α2hpν/4πεoと表される。ここで、α= 分子の分極率、hp = プランク定数、ν = 分子のゆらぎの固有振動数、εo = 真空の誘電率である。
Hamakerによるコロイド粒子間相互作用エネルギーの導出には以下のような問題点がある。
(1)「粒子間力=分子間力の総和」の近似は分子密度が希薄な場合は良い近似であるが高密度の凝縮系ではこの近似は良くない。とくに、粒子の構成原子の分極率αは金属の場合、電子は個々の原子から離れて自由電子になるので意味を失う。
(2)ゆらぎ振動数は一つではない。
(3)分子間van der Waals引力エネルギー-C/r6の表現ではゆらぎ双極子のつくる電場を静電場とみなしているが、分子から遠ざかると双極子のつくる電場は電磁波になり、分子間距離が電磁波の波長程度離れると相互作用の伝播に遅れが生じる(遅延効果)。
この結果、分子間van der Waals引力エネルギーは1/r6ではなく1/r7に比例するようになり、平板状粒子間のvan der Waals引力エネルギーも1/h2ではなく1/h3に比例する。これらの問題をすべて解決したのがLifshitz理論(1956)である。
Hamaker理論はコロイド粒子を多数の分子の集合体と考えるミクロな理論であったが、Lifshitz理論では、コロイド粒子をマクロな物体(連続体)とみなし、個々の分子のゆらぎ双極子静電場を考えるかわりに、粒子内に絶えず発生するゆらぎ電磁場を考える(図1)。この結果、分極率αと分子密度のNにかわって、比誘電率εr登場する。LifshitzはLandauとの共著「ランダウ-リフシッツの理論物理学教程」で知られるロシアの物理学者であるが、この理論の論文は11頁におよび、あまりにも難解であったため、長くコロイド界面化学の分野になじめなかった。しかし、van Kampenら(1968)がたった2頁のNoteで同じ結果を得てから多くの系に適用されるようになった。彼らは、Lifshitzのように平板間の力を直接計算するのではなく、ゆらぎ電磁場に伴う零点振動のエネルギーhpν の総和から求めた。
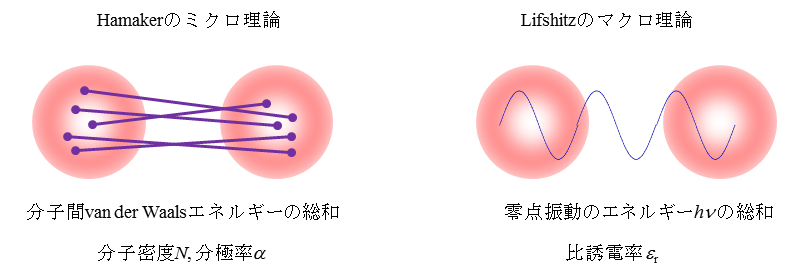
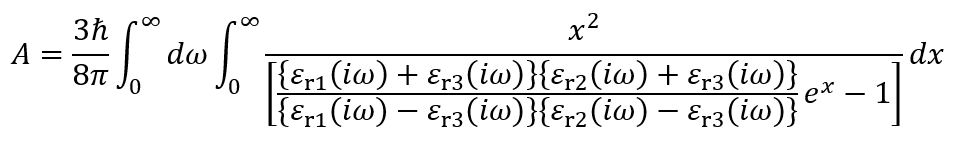
図1 Hamakerのミクロ理論とLifshitzのマクロ理論およびLifshitz 理論によるHamaker定数の表現
図1には、平板間距離が波長より短く遅延効果が無視できる場合のLifshitz理論によるHamaker定数Aの表現を与えてある(ただし、ω = ν/2πは角振動数、ℏ = hp/2π)。比誘電率εr3の媒質を挟む粒子1(比誘電率εr1)と粒子2(比誘電率εr2)の系に適用される。比誘電率はいずれも角振動数ωの関数である。 この式は分子密度Nが小さい場合、Hamakerによる表現A = π2CN2に帰着し、金属の場合はA≈ (3/16√2) ℏωpが得られる。ここで、ωpはプラズマ角振動数と呼ばれる量である。

