第20回 Smoluchowskiの式
前回のコラムで述べたように,コロイド粒子分散系における界面動電現象はいずれも粒子のゼータ電位ζ に関係する。とくに外場が弱い場合には,界面動電現象に基づく測定における種々の測定量(電気泳動移動度や沈降電位等)はゼータ電位に比例する。したがって,界面動電現象の測定からコロイド粒子のゼータ電位を評価することができる。ここで,重要なことであるが,ゼータ電位は物体の重量やサイズのように直接測定される量ではなく,電気泳動移動度や沈降電位等から適切な理論式を用いて計算される量である。理論式が異なれば,同じ測定量から異なるゼータ電位の値が見積もられる。したがって,測定条件に合致した最も適切な理論式を選択する必要がある。
代表的な界面動電現象である電気泳動を考えよう。外部電場Eの下で液体媒質中を速度Uで電気泳動する粒子の電気泳動移動度μはμ = U/Eで定義される。電気泳動移動度μの測定値からゼータ電位ζを計算する理論式はいくつか導かれている。その中で最も広く使われる式はポーランドの物理学者Smoluchowski(Marian Ritter von Smolan Smoluchowski, 1872-1917)の式である。電解質水溶液(比誘電率εr, 粘度η)の中を電気泳動する球状粒子(半径a)の電気泳動移動度μに対するSmoluchowskiの式は次式で与えられる(εo =真空の誘電率)。

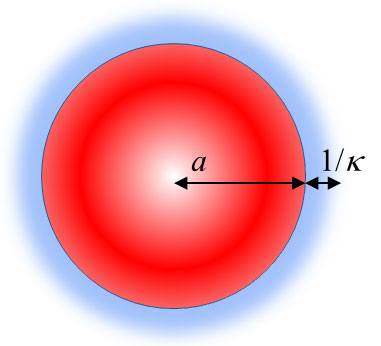
図1 拡散電気二重層 (厚さ1/κ) で囲まれた球状粒子(半径a)。
電気二重層が粒子半径に比べて十分薄い場合(a »1/κすなわちκa »1),
粒子表面を平面とみなせる。
電解質溶液中で帯電粒子は拡散電気二重層と呼ばれるイオン雲(主として対イオンからなる)に囲まれている(第4回コラム参照)。Smoluchowskiの式(1)は拡散電気二重層が粒子サイズに比べて十分薄く粒子表面を事実上平面とみなせる場合に適用できる。実は, (1)式は粒子の形状に依存せず,円柱状粒子や楕円体粒子であっても適用できる。(1)式は次のように導かれる。
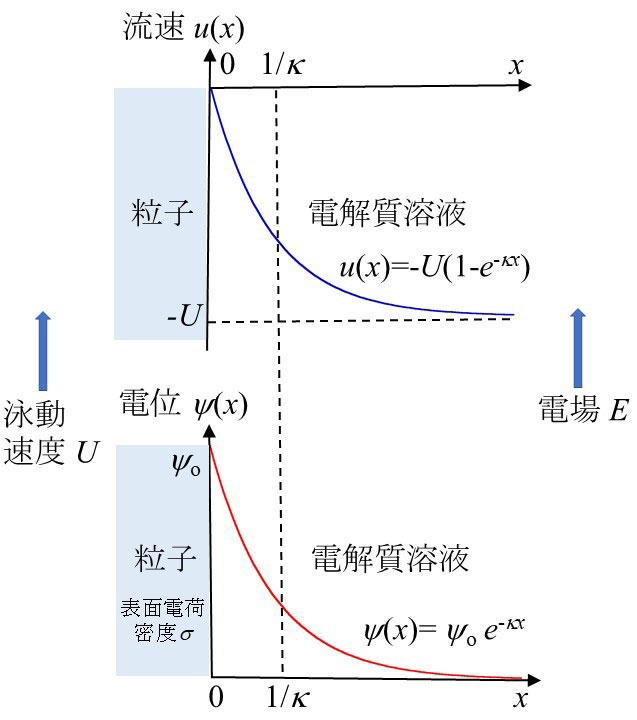
図2 電場Eの下で速度Uで泳動する平板の周囲の流速分布u(x)と電位分布 ψ(x)
図2のように粒子から見た流速分布u(x)は電位分布ψ(x)と同じように指数関数的に変化し,表面からデバイ長1/ 程度離れるとほぼ-Uに等しくなる。したがって,粒子表面における速度勾配の大きさdu/dxはU/(1/κ)=κUにほぼ等しい。したがって,粒子表面に働く粘性力ηdu/dx(単位面積当たり)はηκUである。
一方,粒子表面の電荷密度をσとすると表面に働く電気力は単位面積当たりσEになる。粒子が一定速度Uで電気泳動する定常状態では粘性力と電気力がつり合うため, ηκU=σEである。このつり合いの式から,電気泳動移動度μ = U/Eはμ =σ/ηκのように得られる。
この式に表面電荷密度σと表面電位ψoを結びつける式ψo=σ/εrεoκ(第4回コラムの(1)式でκa »1とすると得られる)を代入し,かつψo =ζと近似すると(1)式になる。以上の(1)式の導出では近似式を用いたが,問題を厳密に解いても同じ結果が得られる。

