第18回 熱力学第1法則と内部エネルギー

多数に分子からなる物体のエネルギーは外部エネルギーと内部エネルギーの和であり、それぞれのエネルギーはさらに運動エネルギーとポテンシャルエネルギー（位置エネルギー）の和で与えられる。

物体の重心が静止し、かつ他の物体との相互作用（物体に働く重力等）を考えなければ、物体のもつエネルギーは内部エネルギーのみになる。静止物体の内部エネルギーは構成分子の運動エネルギーと分子間力のポテンシャルエネルギー（分子間力に逆らっている度合い）の和である。分子間にはvan der Waals引力が働くので、分子間距離が大きくなると分子間力に逆らうことになるので、分子間力のポテンシャルエネルギーは増加する。

静止物体の構成分子の運動は無秩序で不規則な運動すなわち熱運動である。物体が静止しているので、分子の規則的な運動はない（あれば、物体が動き出してしまう）。物体のもつ無秩序な運動の運動エネルギーは熱エネルギーとよばれる。分子間に力が働かない理想気体を考えると、その内部エネルギーは熱エネルギーそのものになる。

物体の内部エネルギーEは外部から仕事Wをされるか熱Qを受けとると熱力学第一法則にしたがってΔE= W + Qだけ増加する。一般に仕事は加えた外力×物体の移動距離に等しい。重力が働くために落下しようとする物体を重力に逆らって手で持ち上げると、手の力のした仕事が物体の重力ポテンシャル（重力の位置エネルギー）の上昇に等しくなる。ここで、速く持ち上げると物体が飛び上がって、手のした仕事の一部が物体の運動エネルギーになってしまうから、ゆっくりと持ち上げなければならない（準静的過程、可逆過程）。

しかし、静止物体に力を加えて移動させると、物体が動いてしまう。物体の重心を静止させたまま、物体に仕事を加える方法が二つある（図1）。(1)物体を圧縮するか（体積の減少）、(2)物体を分割すればよい（表面積の増加）。
ただし、物体の圧縮の場合は、必然的に表面積の減少も伴う。さて、(i)物体は一般に自分の体積を増加させようとする（そうでないなら、物体はとっくに消滅してしまうだろう）。また、(ii)物体は一般に自分の表面積を減少させようとする（このために、液滴は表面積最小の球形になる）。(i)と(ii)の傾向がつりあって、物体のサイズが決まる（図2）。

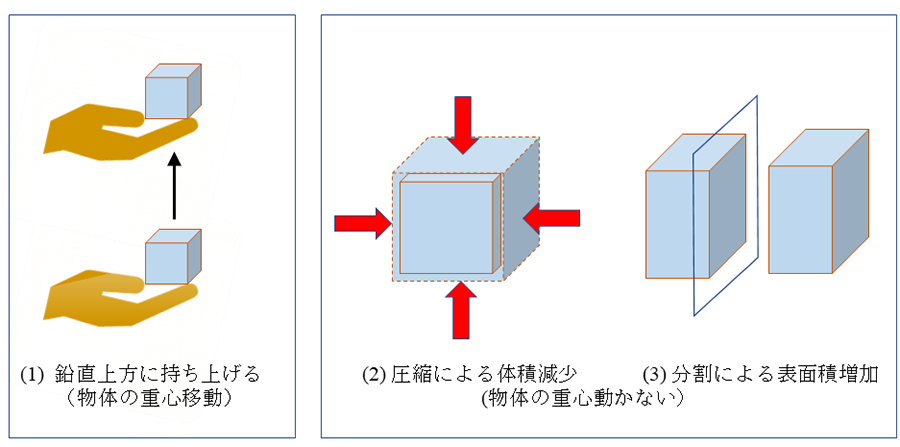
図1 物体の重心を移動させない仕事

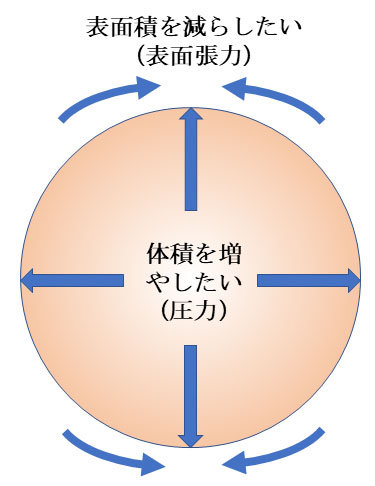
図2 圧力と表面張力のつり合いで物体のサイズが決まる。

落下したい物体の意思に逆らって、物体を手で持ち上げると物体に仕事をして、その分物体のポテンシャルエネルギーが増加する。同様に、膨張したがっている物体をその意思に逆らって手で押さえつけ圧縮すると物体に仕事をしたことになり、物体の内部エネルギーが増加する。したがって、物体の体積がΔV減少したとき、W = -(圧縮に対する抵抗)×ΔVと書ける。ここで、右辺の負符号は体積減少のときに手は仕事をし、体積増加のときは逆に手が仕事をされることに対応している。さらに、圧縮に対する抵抗が物体の圧力Pであるから、W = -PΔVと書ける。一方、物体は自分の表面積を減らしたいので、その意思に逆らって手で表面を引き延ばして表面積を増加させると、物体の内部エネルギーが増加する。
したがって、物体の表面積がΔa増加したとき、W = +(引き伸ばしに対する抵抗)×ΔAと書ける。ここで、右辺の正符号は表面積増加のときに手は仕事をし、表面積減少のときは逆に手が仕事をされることに対応している。さらに、引き延ばしに対する抵抗を物体の表面張力γとよぶ。したがって、W = γΔAと書ける。以上をまとめると、W = -PΔV + γΔAと表される。