第12回 一定表面電位モデルと一定表面電荷密度モデル

DLVO理論（第6回）における2球の静電相互作用エネルギーの計算では、(i) まず2平板間の中央の点の電位を1枚の平板のつくる電位の2倍で近似して平板間相互作用エネルギーを求め（線形重畳近似）、(ii) 次にDerjaguin近似を用いて2球の静電相互作用エネルギーを計算した。この結果、Schulze-Hardyの経験則の説明に成功した。しかし、この線形重畳近似は平板間距離hが大きいときのみ有効であって、厳密には、2枚の平板が接近に伴う電位分布の変化（hが小さい場合）のモデル依存性を考慮すべきである。

代表的な2つのモデル、すなわち、一定表面電位モデルと一定表面電荷密度モデルが提出されている。DLVO理論では、ヨウ化銀粒子のようにヨウ素イオンまたは銀イオンの吸着によって粒子の表面電位が決まる場合を想定して、一定表面電位モデルを採用している。したがって、2枚の平板の接近につれて、表面電位を一定に保つために表面電荷密度の減少すなわち放電（吸着イオンの脱着）が起きる。もし、放電過程よりも早く2粒子が接近する場合は、放電が間に合わず、一定表面電位モデルよりも一定表面電荷密度モデルの方が適している。また、粒子の表面電荷が吸着でなく表面に存在する解離基による場合、やはり、一定表面電荷密度モデルの方が適している。図1に両モデルによる平板間電位分布の変化と図2と図3に表面電荷密度（図2）および表面電位（図3）の変化を示した。

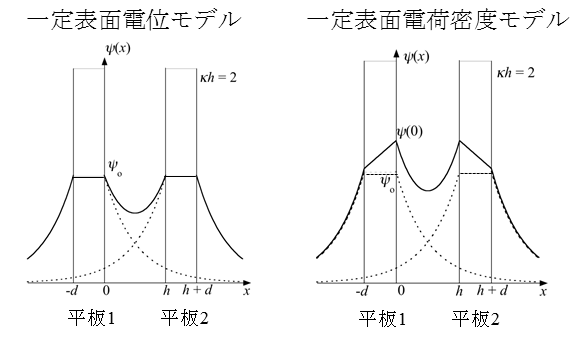
図1 両モデルによる平板間電位分布の変化

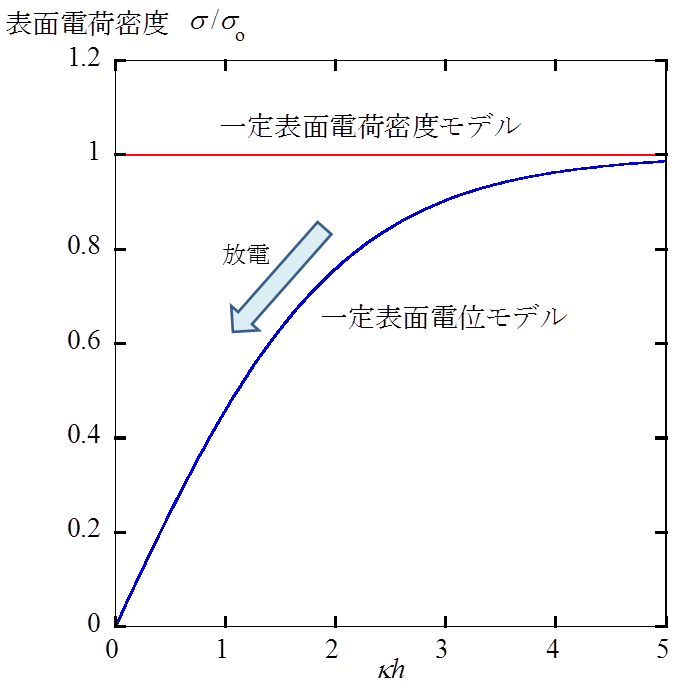
図2 両モデルによる表面電位の変化

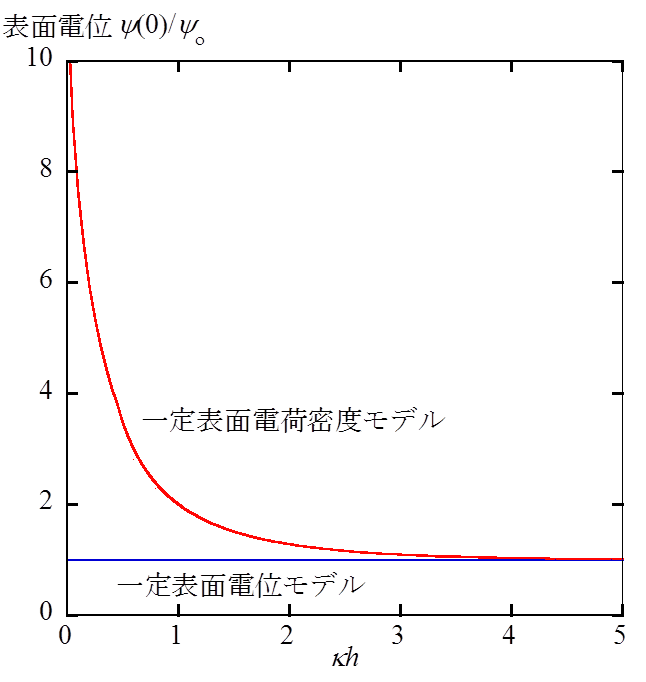
図3 両モデルによる表面電荷密度の変化

一定表面電位モデルでは2つの平板の接近とともに放電が起こり表面電荷密度が減少し、平板間距離h → 0で表面電荷密度がゼロ（完全放電）になる。一方、一定表面電荷密度モデルでは、表面電荷密度を一体に保つために、表面電位が平板の接近とともに急激に上昇する。さらに、このモデルでは平板接近とともに平板間に電位勾配すなわち電場が誘起される。したがって、平板間静電相互作用の力およびエネルギーは一定表面電荷密度モデルの方が大きい。両者の違いが著しくなるのはhがDebye長より十分小さい場合で、分散安定性の厳密な評価（安定度比の計算）にはモデルの違いを考慮する必要がある。DLVO理論（第8回(1)式）ではモデル依存性は考慮されていないにもかかわらず、Schulze-Hardyの経験則の説明に成功したことは注目に値する。

さらに、表面解離基の解離度の表面電位依存を考慮したモデルがある。表面電位と表面電荷密度の両方が一定ではなく平板間距離の関数になり、解離平衡の式から両者が決まる。電荷調節モデルと呼ばれる。また、粒子表面がイオン浸透性の厚い高分子電解質層で覆われている粒子（柔らかい粒子と呼ばれる）の場合、層深部の電位はDonnan電位に常に等しく平板間距離に依存しない。Donnan電位制御モデルと呼ばれる。