第25回 Henryの式と粒子の表面電荷密度
球状粒子(半径α)の電気泳動移動度μに対するHenryの式 (前回コラムの(1)式)では、μは粒子のゼータ電位ζ に比例する。すべり面を表面とみなせば、ゼータ電位ζ は表面電位ψoに一致する(第19回コラム)。ここで、ヨウ化銀粒子のように媒質から粒子表面への(Ag+またはI-イオン)の吸着で粒子の表面電位ψoが決定される場合(この場合の吸着イオンを電位決定イオンとよぶ)、ψoはNernstの式に従って電解質濃度に依存しない一定の値をとる。しかし、表面の電荷がそこに存在する解離基に由来する場合は、ψoは電解質濃度(したがって、Debye-Hückelのパラメタκ)に依存するようになる。表面電位が低い場合のψoは次式で与えられる(第4回コラムの(1)式)。
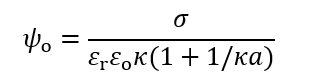 (1)
(1)
上式はκα→0の極限で、ψo= ασ/εrεo= Q/4πεrεoαに近づく(Q = 4πα2σは粒子表面の総電荷量)。これはクーロン電位である。
図1にψoのκα依存を与えた(ただし、ψo*=ψo /(ασ/εrεo))。κα増加とともに電解質イオンの遮蔽効果により、ψo は減少しゼロに近づく。Henryの式 (前回の(1)式)において、ζを(1)式のψoで置き換えると、Henryの式は以下のようになる。
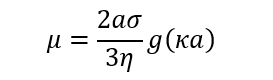 (2)
(2)ただし、g(κα)は次式で与えられ、μとσを直接結びつけるHenry関数である。
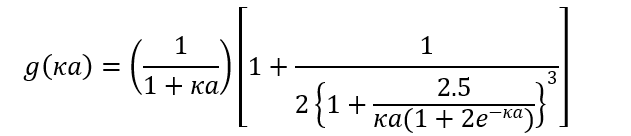 (3)
(3)図2にg(κα)をκαの関数として与えた。前回コラムの図1のf(κα)とだいぶ様子が異なることがわかる。しかし、前回コラムの図1と同様に、καが大きいほど(図の右方)電気二重層は薄くかつ電気二重層内の電解質イオン濃度は高く遮蔽効果が大きい。καが小さいほど(図の左方)電気二重層は厚くかつ電気二重層内の電解質イオン濃度は低く遮蔽効果が小さい。κα→0の極限で電気二重層は無限に厚くなるが同時に電解質濃度→0となって電気二重層は消失する。
通常は電気泳動移動度の測定からゼータ電位を計算で求めることが目標であるが、これはコロイド分散系安定性の評価の際にDLVO理論に登場する粒子間相互作用エネルギーがゼータ電位で表されることに対応している(第8回コラム)。しかし、電気泳動移動度の測定からゼータ電位を求めることが最終目的ではなくさらに、(1)式を用いて、粒子の表面電荷密度σまで求める必要が生じる場合もある。そのような場合に今回登場したHenry関数が有効になるであろう。
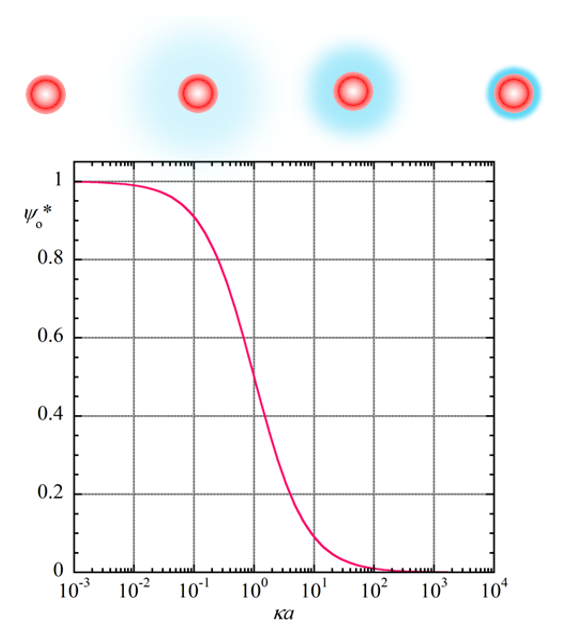
図1. 球状粒子の表面電位ψoのκα依存
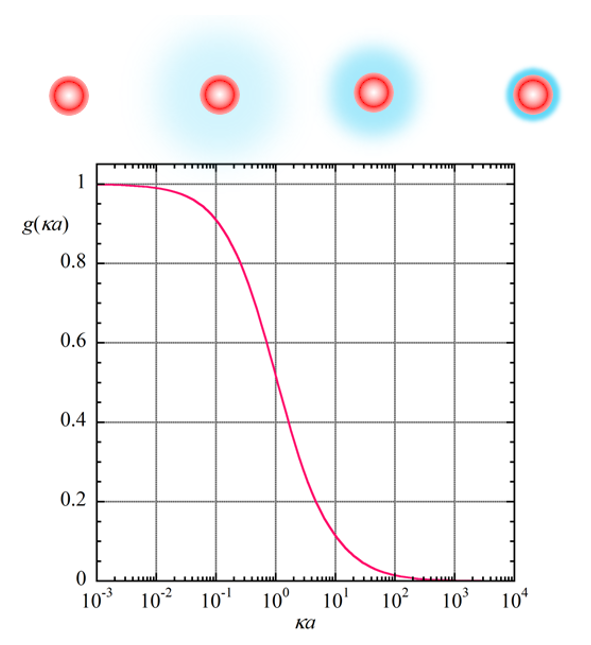
図2. ゼータ電位のκα依存を考慮したHenry関数

