第4回 帯電粒子周囲のイオン雲 - 拡散電気二重層とDebye長
電解質水溶液中の帯電コロイド粒子の表面周囲では、粒子の表面電荷と反対符号をもつイオン(対イオン)がクーロン力によって引きつけられ濃度が高くなる。イオンは同時に熱運動を行っているため、イオン分布は拡散構造(雲状)になる。一方、粒子表面と同符号のイオン(副イオン)は粒子表面から反発されて濃度が低い。このように帯電粒子は裸ではなく、拡散電気二重層とよばれるイオン雲で囲まれている。コロイド粒子の挙動は電気二重層の存在に大きく依存し、とくにその厚さが重要な働きをする。電気二重層の厚さは1/κで与えられ、Debye長とも呼ばれる。κ はDebye-Hückelのパラメタである。粒子周囲の電位分布はPoisson-Boltzmann方程式の解として与えられ、イオン分布も決める。図1は球状粒子周囲の対イオン濃度分布の計算例である。
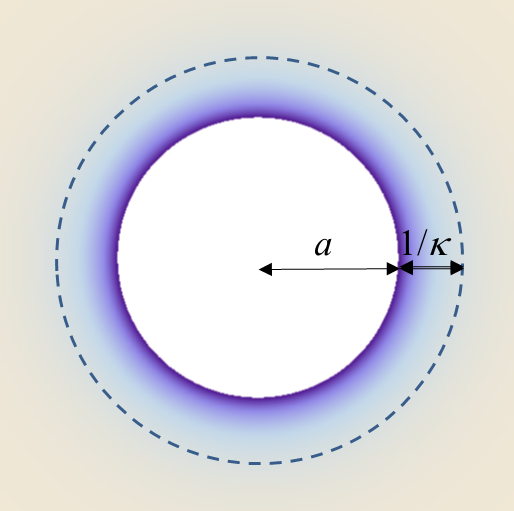
図1. 球状粒子(半径α) 周囲の対イオン濃度分布. 1/κ=Debye 長. 表面電位25mV,κα=2の場合.
Mathematica DensityPlotによる計算 (濃度の高低を濃淡で表す). 25℃.
電位が低いとき、半径αの球状粒子の表面電位ψoと表面電荷密度σの関係は次式で与えられる。
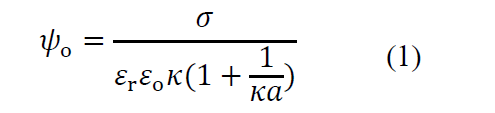
あるいは、粒子の表面電荷の総量Q=4πα2σを用いると、(1)式は次のように書き換えられる。
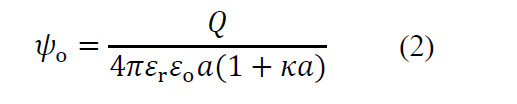
ここで、εo= 真空の誘電率、εr= 溶液の比誘電率、また、表1にDebye長1/κの値を与える。
とくに、価数z、数密度n (m-3) の対称型電解質の場合、κ= (2z2e2n/εrεokT)1/2で与えられる。ここで、NA= Avogadro数、e= 素電荷、k= Boltzmann定数、T= 絶対温度である。電解質濃度として、モル濃度C(M)を用いる場合、n= 1000NAC を用いて、nをCで置き換えればよい。
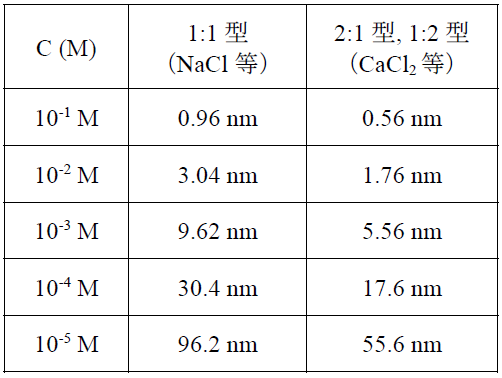
表1 種々の電解質の型と濃度におけるDebye長 (25℃)
(1)式または(2)式が示すように、σからεoを求めるためにはκの値を正確に求めておく必要がある。ただし、有機溶媒のような非水系の場合は、電解質イオンは存在しないか、存在しても極めて微量なので、κの値を正確に求めることは容易ではない。しかし、καの値が非常に小さいので(κα << 1)、 (2)式右辺の分母の(1+κα)は1で置き換えてよく、(2)式はクーロン電位ψo= Q/4πεrεoαで十分近似できる。したがって、このような場合、κの値を正確に見積もる必要はなくなる。

