第46回　濃厚分散系と桑原セルモデル

これまでのコラムでは液体媒質中での単一のコロイド粒子の界面動電現象を扱ってきた。粒子が多数存在する濃厚系の場合は粒子間相互作用を考慮しなければならない。粒子間相互作用には流体力学的な相互作用と電気的な相互作用がある。粒子の表面間距離がDebye長に比べて大きい場合、粒子間静電相互作用の寄与は小さい。このような場合の濃厚分散系における電気泳動理論では図1のようなセルモデルが用いられる。このモデルでは、球状粒子の場合、半径αの各粒子を半径bの仮想的なセルでそれぞれ囲む。このとき、φ= (α/b)³をこの系における粒子の体積分率とみなす。セルとセルの間にできた隙間は無視する。流速のセル表面における境界条件としてHappelの「自由表面モデル」と桑原の「渦無しモデル」があるが、界面動電現象で正しい結果（κα→∞ の極限で、Smoluchowskiの式に帰着）を与えるのは桑原モデルである。単一粒子の場合、液体媒質は無限に拡がっているが、濃厚系では個々の粒子の占有体積は他の粒子の存在によって制限を受け、各粒子の属するセル内に閉じ込めあれる。この結果、セル内では必然的に液体の回転運動（渦運動）が生じる。この回転の大きさと向きを表すベクトルが渦度である。図2のように互いに接する2つのセルを考えると、図2の黄色部分の回転の向き左回り（渦度< 0）であり、緑色部分の回転の向き右回り（渦度> 0）である。したがって、隣り合うセルの接する部分の渦度はゼロ（渦無し）でなければならない。これが桑原セルモデルである。

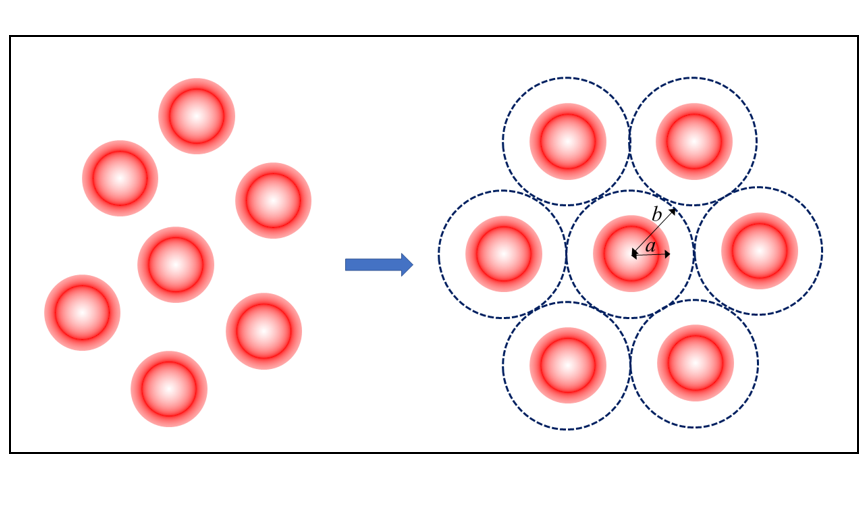図1. 濃厚分散系とセルモデル

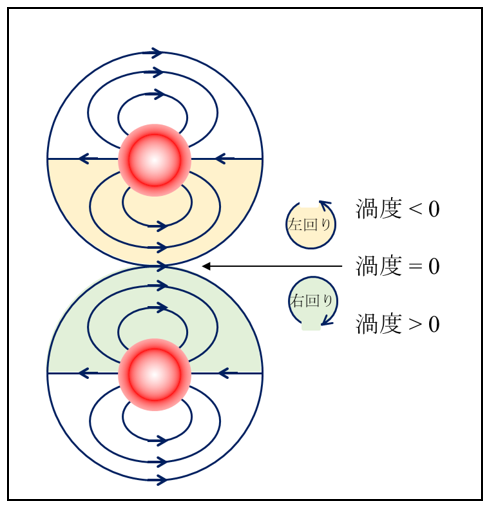図2. 桑原セルモデル

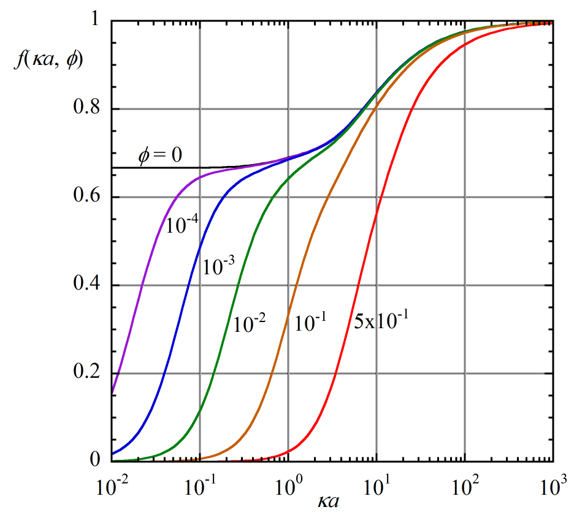
第24回コラムで球状粒子に対するHenryの式について述べたが、図3には体積分率φのコロイド粒子濃厚系におけるHenry関数ƒ(κα, φ)をκαの関数として示した（H. Ohshima, J. Colloid Interface Sci., 188, 481–485 (1997))。φ=0の曲線が希薄系のHenry関数である。κα→∞ の極限で、ƒ(κα, φ)→１すなわちSmoluchowskiの式に帰着する（Happelモデルではそうはならない）。φ= 1%以下であれば、κα >1でƒ(κα, φ)のφ依存すなわち濃厚系の効果は小さいことがわかる。