第24回 Smoluchowskiの式とHückelの式をつなぐHenryの式

Smoluchowskiの式とHückelの式をつなぐ式が以下のHenryの式である。液体媒質 (比誘電率ε_r, 粘度η, Debye長1/κ) 中を泳動する球状粒子(半径α, ゼータ電位ζ) の電気泳動移動度μに対するHenryの式は次式で与えられる。

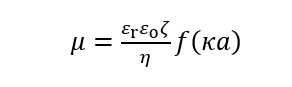　　　 (1)

ここで、f(κα)はHenry関数と呼ばれ、κα→0でf(κα)→2/3であり、(1)式はHückelの式になる。また、κα→∞でf(κα) →1であり、(1)式はSmoluchowskiの式になる。このようにHenryの式はSmoluchowskiの式とHückelの式をつなぐ式である。Henryの導いたf(κα)は指数積分を用いた複雑な式であるが、以下の近似式が導かれている¹⁾。

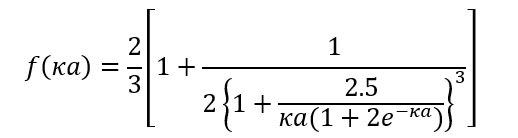　　　 (2)

(2)式は以下のように簡単に導くことができる。前回のコラムの(2)式で示したように、粒子の存在による外部電場の歪みに対応して、位置 (r, θ) の電位が-Ercosθから -Er(1+α³/2r³)cosθまで1+α³/2r³倍に増加する。
Debye長1/κの厚さをもつ電気二重層中のイオン分布の重心のr座標をr ≈ α+δ/κと表し（δは1~2程度の大きさの数）、r を重心の座標α+δ/κで置き換えると、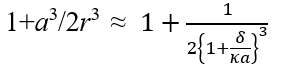になる。
さらに、厳密解とよく一致するようにδ=2.5/(1+2e^-κα)と選んだ結果得られた式が(2)式である。

図1にHenry関数をκaの関数として与えた。すべてのκαの値に対して、Henryの式が適用できるが、とくに、κα < 0.3ではHenryの式を使わずに、Hückelの式を適用でき、κα > 200ではSmoluchowskiの式が適用できることがわかる。このように、コロイド粒子の電気泳動移動度μの測定値から電気泳動移動度μを計算する際に、καの値をきちんと求めておくことが肝要である。

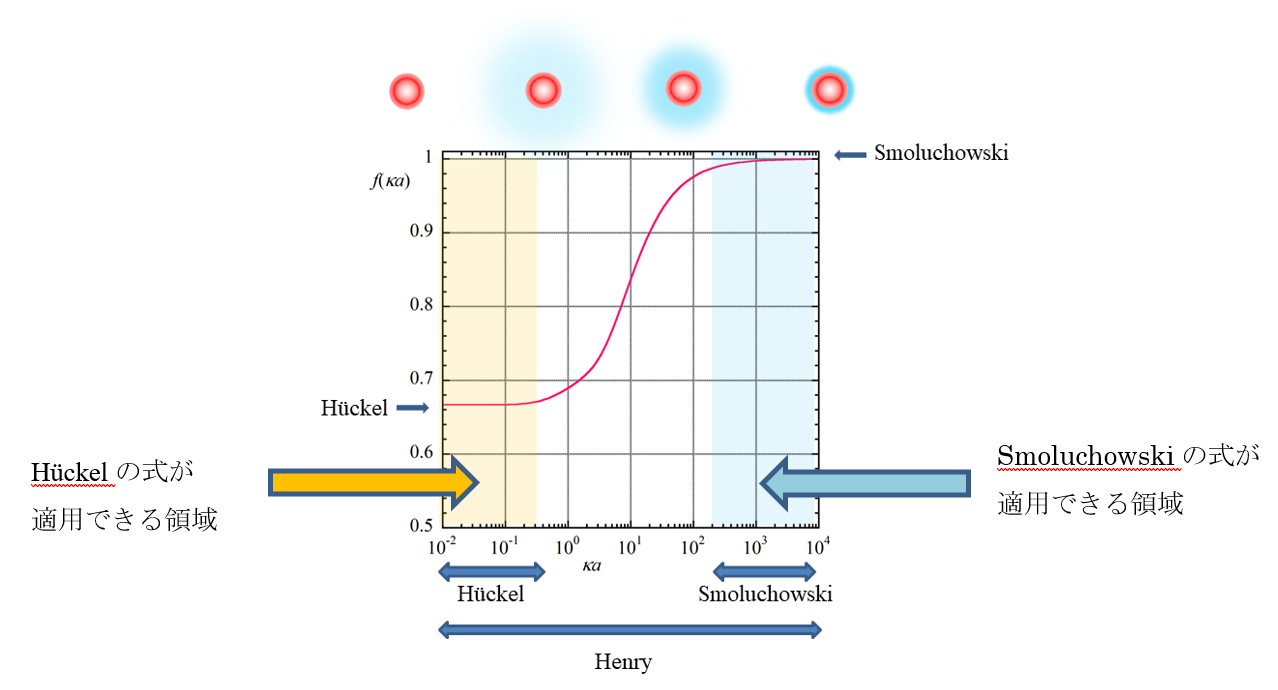
図1. Henry関数f(κα)

καが大きいほど（図の右方）電気二重層は薄くかつ電気二重層内の電解質イオン濃度は高く遮蔽効果が大きい。 καが小さいほど（図の左方）電気二重層は厚くかつ電気二重層内の電解質イオン濃度は低く遮蔽効果が小さい。 κα→0の極限で電気二重層は無限に厚くなるが同時に電解質濃度→0となって電気二重層は消失する。

《文献》 H. Ohshima、A Simple Expression for Henry's Function for the Retardation Effect in Electrophoresis of Spherical Colloidal Particles, J. Colloid Interface Sci., 168, 269-271 (1994).