第47回 非水系(無塩系)の電気泳動と対イオン凝縮
第22回コラムで電解質濃度ゼロの場合(非水系)におけるコロイド粒子の電気泳動移動度に適用できるHückelの式について述べた。しかし、ここで注意すべきことがある。コロイド粒子が分散した電解質溶液中には、添加した電解質由来の対イオン(粒子と同符合のイオン)と副イオン(粒子電荷と同符号のイオン)の他に、粒子そのものに由来する対イオンが存在する。たとえば、もともとの粒子表面にカルボキシル基がNa塩の形で存在し、この解離から生じたNa+イオンが粒子由来の対イオンである。この対イオンは、電解質を加えなくても、系の電気的中性条件のために、媒質中に必ず存在する。添加電解質イオン濃度ゼロの系はすべてのイオンが全く存在しない系ではなく、粒子由来の対イオンのみ存在する系である。このような系は、無塩系または無添加塩系と呼ばれる。無塩系では対イオン凝縮という特異な現象が起きる。 この現象は今井・大沢理論によって詳しく調べられた。今井・大沢理論から、半径αの球状粒子電荷Qに臨界値Qcrが存在することが明らかになった(ただし、η= 媒質の粘度,εr= 媒質の比誘電率,εo= 真空の誘電率)。Qcrは以下の(1)式で与えられ、粒子の体積分率φに依存する。
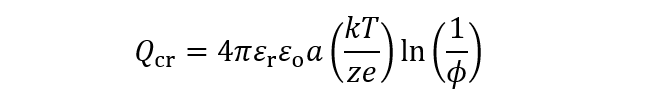 (1)
(1)今井・大沢理論に基づいて無塩系における粒子のゼータ電位ζと電気泳動移動度μを求めると以下のようになる (H. Ohshima, J. Colloid Interface Sci, 248, 499-503 (2002))。 低電荷の場合(Q < Qcr)は以下のように対イオン凝縮はまだ起きずにゼータ電位ζはクーロン電位に一致し、電気泳動移動度μはHückelの式で与えられる。
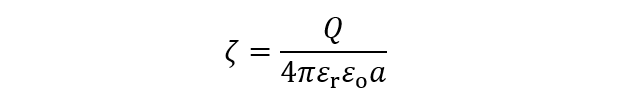 (2)
(2)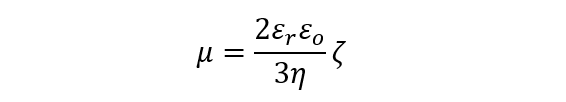 (3)
(3)しかし、高電荷の場合(Q≥Qcr)は粒子表面のごく近傍に、ある量の対イオンが凝縮し、粒子の実効電荷QeffはQcrになる。すなわち、Qをいくら増やしてもQeffはQcrのまま一定である。つまり、低電荷の場合は、媒質中に自由な対イオンのみ存在し、その数はQとともに増加する。しかし、高電荷の場合は対イオン凝縮のために、凝縮した対イオンの数のみがQとともに増え、自由な対イオンの数は一定である。この結果、次式で与えられるように粒子のゼータ電位は見かけの実効ゼータ電位ζeffに等しくQに依存せず一定になる。電気泳動移動度μも対イオン凝縮が起きるとμmaxに達したまま一定になる (図1)。
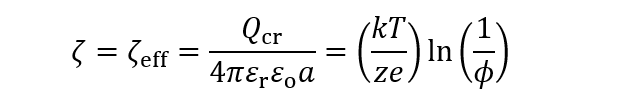 (4)
(4)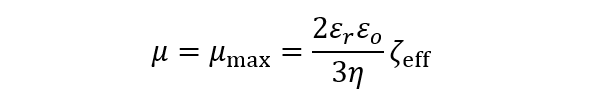 (5)
(5)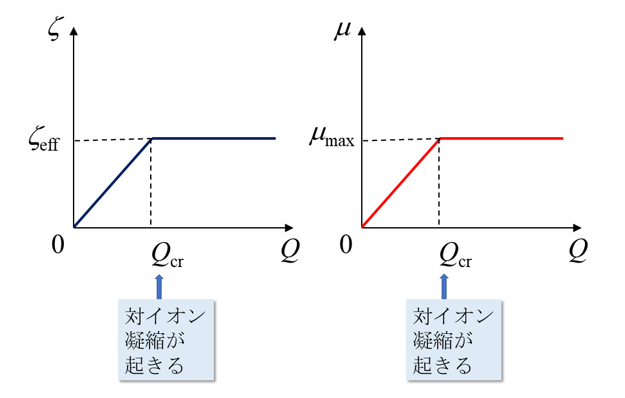
粒子の電荷Qが臨界値Qcrより大きくなると対イオン凝縮が起きる。
Q ≥ Qcrではゼータ電位ζと電気泳動移動度μがともに粒子の電荷Qに無関係に一定になる。

