第32回 多孔質体に働く Stokes抵抗

多くの細孔を含む多孔質（ポーラス）の粒子の界面電気現象はどうなるであろうか。多くの粒子が互いに凝集してできた凝集体（フロック）や球状あるいは円柱状の高分子も多孔質体として扱うことが可能である。Darcyは多孔質体にx方向の圧力勾配dp/dx（p =圧力）を加えると、その結果生じた水の流速uが経験式u= -(k/η)dp/dxに従うことを見出した。ここで、ηは水の粘度、kは透過率（あるいは透水係数）である。後になって、BrinkmanおよびDebyeとBuecheはDarcyの式が以下のNavier-Stokes式の特別な場合であることを明らかにした。

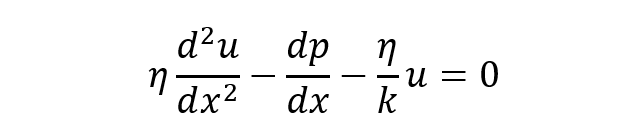(1)

(1)式で左辺第1項を無視するとDarcyの式が得られる。透過率kの平方根を1/λとおくと（すなわち、1/λ = $\sqrt{k}$）、1/λは長さの次元をもち、Brinkmanの遮蔽長とよばれる。λが大きいほど多孔体の中を水が透過しにくい。図1に球状の多孔質粒子（半径α）内外の流線分布を与えた。粒子内部で液体の流動が起こる点で、第28回コラムで扱った液滴と同様であるが、大きな違いがある。液滴の場合、液滴内外で液体は交換せず、液滴内部の液体は常に液滴内に閉じ込められている。このため、液滴内で液体は回転する。一方、多孔性粒子の場合は、粒子内外で粒子が移動するたびに液体が粒子内外で次々と入れ替わっている。

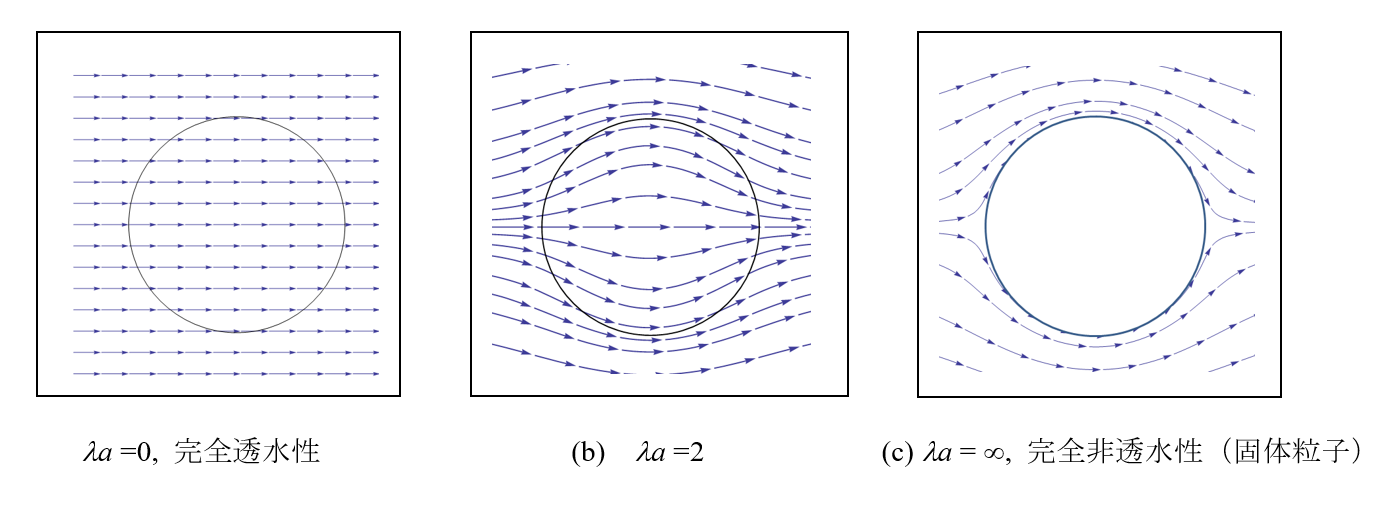
多孔質の球状粒子（半径α）に働くStokes抵抗は(1)式をもとに次式のように計算される。

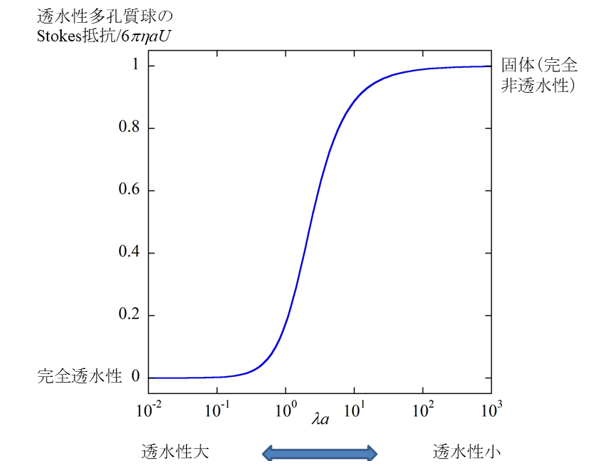
(2)

図2は(2)式をもとに計算した多孔質の球状粒子に働くStokes抵抗である。粘度ηの水中を速度Uで動く粒子に働くStokes抵抗が固体粒子の場合に比べてどう変化するか示す。図2よりλα>10で多孔質粒子は固体粒子として（Stokes抵抗=6πηαU）、λα< 0.1では逆に完全透水性粒子として扱える（Stokes抵抗ゼロ）ことがわかる。このように多孔質粒子に働くStokes抵抗は固体粒子のStokes抵抗からゼロまで大きく変化することがわかる。速度Uで液体媒質中を動く半径αの液体粒子のStokes抵抗の場合、6πηαU（固体）から4πηαU（気泡）まで最大で2/3倍の変化である。