第41回 ゼータ電位が高い場合のHenry関数の改良
前回コラムで述べたように、電解質水溶液中(比誘電率εr, 粘度η)の球状コロイド粒子の電気泳動の標準理論はSmoluchowskiに始まり、Hückel, Henry, Overbeekを経てO’BrienとWhiteによって完成した。この理論によれば、電気泳動移動度μは粒子の半径αとゼータ電位ζ、溶液のDebye- Hückelパラメタκ (逆数1/κ= 電気二重層の厚さ)のみならず、電解質イオンの抵抗係数にも依存する。したがって、μは電解質の種類によって変わることになる。図1にはO’Brien-White理論に基づいて、いくつかのκαに対して数値計算した KCl水溶液中(25℃)における無次元電気泳動移動度
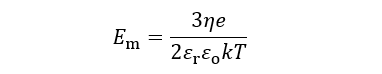 (1)
(1)を無次元ゼータ電位eζ/kTの関数として与えた(εo= 真空の誘電率)。図1においてκα= ∞とκα= 0の直線はそれぞれ、Smoluchowskiの式(Em= 3eζ/2kT)とHückelの式(Em= eζ/kT)に対応する。これらの2直線に挟まれた領域がHenryの式(Em= eζ/kT・f(κα))であるf(κα)= Henry関数、第24回コラム(2)式)。さらに、この図からeζ/kT≤2(室温ではζ≤ 50mV)では数値計算の結果はほぼ直線になるので、Smoluchowski、Hückel, Henryの式が適用できることがわかる。
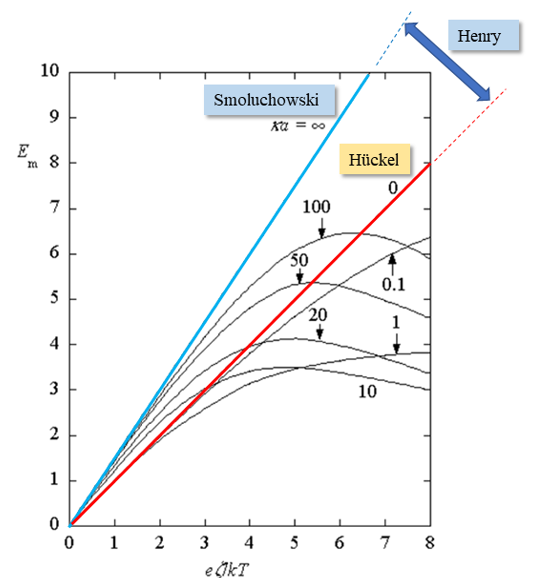
無次元電気泳動移動度Emと無次元ゼータ電位eζ/kT
図1の横軸はゼータ電位であったが、Henry関数と比較するために図2では無次元電気泳動移動度をκαの関数として与えた。
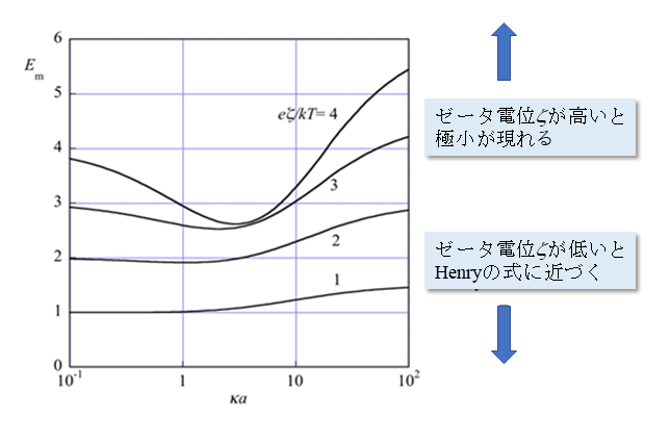
無次元電気泳動移動度Emのκα依存.
ゼータ電位を低くするとHenryの式に帰着する。ゼータ電位が高い場合は、電気泳動移動度に極小が現れる。なお、eζ/kT≤4(室温ではζ ≤100mV)では以下の近似式が適用できる1)。
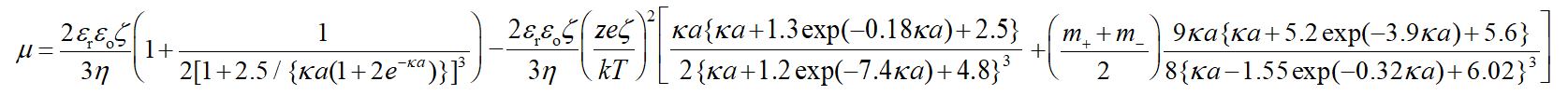 (2)
(2)ここで、m±はカチオンとアニオンの無次元抵抗係数で抵抗係数λ±、拡散係数D±,極限等量伝導度$Λ_±^o$と次式で結ばれる。
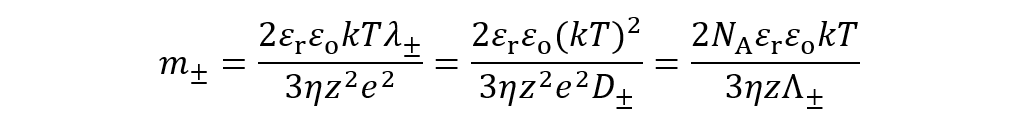 (3)
(3)ここで NA はアボガドロ数である。(3)式右辺の第1項がHenryの式であり、第2項と第3項が補正項である。実は、ζ3の精度まで求めたOverbeekの式が(2)式に対応するが、Overbeekの式には計算の誤りがあり(数値的には最大20%)、(2)式ではその誤りが訂正されている。
文献
- H. Ohshima, J. Colloid Interface Sci., 239, 587–590 (2001)

