第26回 円柱状粒子に対するHenryの式
円柱状粒子の場合、図1のように外部電場Eに平行に泳動する場合と垂直に泳動する場合で電気泳動移動度が異なる。液体媒質 (比誘電率εr, 粘度η, Debye長1/κ) 中を泳動する無限に長い円柱状固体粒子(半径α, ゼータ電位ζ) の電気泳動移動度μに対して、Henryは球の場合と同様の式を導いている。
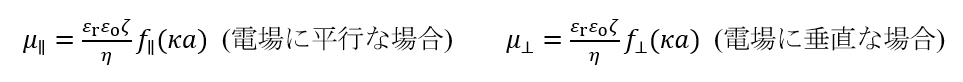 (1)
(1)
ここで、μ‖とμ⊥はそれぞれ粒子が電場に平行および垂直に泳動する場合の電気泳動移動度であり、f‖(κα)とf⊥(κα)は各場合のHenry関数である。図1に円柱および球にHenry関数をκαの関数として与えた。
外部電場は粒子表面に平行に歪められるため、電場に平行な電気泳動の場合、f‖(κα)はすべてのκαに対して1であり、μ‖は常にSmoluchowskiの式で与えられる(μ‖ = εrεoζ/η)。
電場に垂直な電気泳動の場合、κα→0でf⊥(κα)→1/2であり、μ⊥は円柱に対するHückelの式になる(μ⊥ = εrεoζ/2η)。
また、κα→∞ではf⊥(κα)→1であり、μ⊥はSmoluchowskiの式になる(μ⊥= εrεoζ/η)。Henryの導いたf⊥(κα)は複雑な式であるが、以下の近似式が導かれている1)。
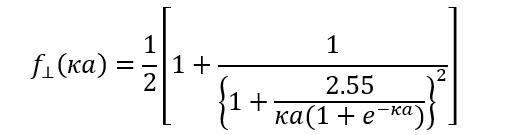 (2)
(2)(2)式も球の場合と同様、粒子の存在による電場の歪みを考えると、簡単に導くことができる。円柱状粒子が電場方向に対して任意の角度で泳動する場合の電気泳動移動度は以下の平均移動度μavの式で計算される。
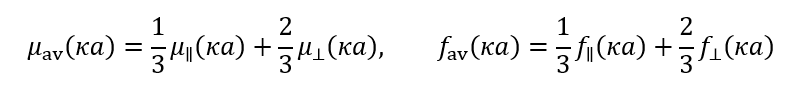 (3)
(3)電場に対して任意の角度で泳動する1個の円柱の電気泳動移動度と多数の円柱が泳動する場合の平均電気泳動移動度は等価である。多数の円柱が電気泳動する場合、全体の1/3が電場に平行に、2/3が垂直に泳動すると考えられるから、(3)式が成り立つ。図2をみると、角度平均をとると円柱の電気泳動移動度は球の場合とあまり変わらないことがわかる。球と全く異なる形状をもつ円柱の電気泳動移動度が平均をとると球の電気泳動に近い値をとることから、円柱以外の形状の粒子の電気泳動移動度も平均をとると球の電気泳動移動度に近い値になることが予想される。
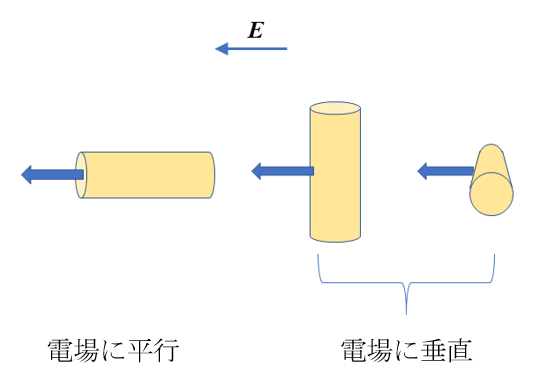
図1. 円柱状粒子の電気泳動
多数の円柱が電気泳動する場合、全体の1/3が電場に平行に、2/3が垂直に泳動すると考える。
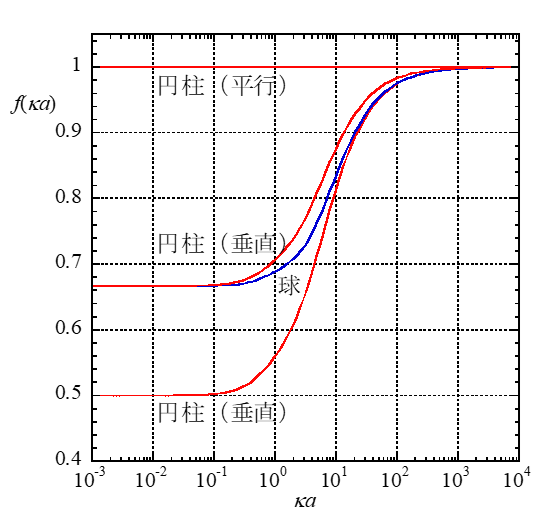
図2. 円柱と球に対するHenry関数f(κα)
《文献》 H. Ohshima、Henry's Function for Electrophoresis of a Cylindrical Colloidal Particle, J. Colloid Interface Sci., 180, 299-301 (1996).

