第43回 円柱状粒子に対する緩和効果
第26回コラムでゼータ電位の低い場合(50mV以下)の円柱状粒子の電気泳動移動度を扱ったが、今回は高ゼータ電位における緩和効果を考慮した電気泳動について述べる。円柱の運動方向が電場に平行か垂直かによって移動度は異なる(図1)。円柱は十分に長く円柱末端の効果を無視できるものとする。
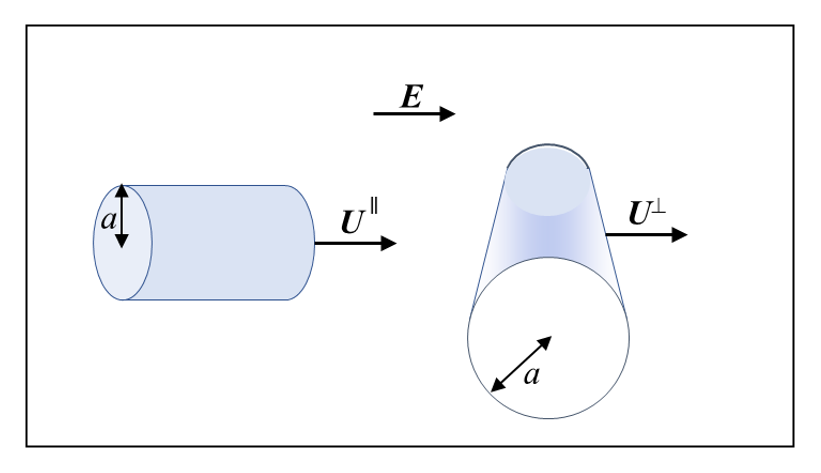
左:電場Eに平行に速度U‖で泳動
右:電場Eに垂直に速度U⊥で泳動
円柱が電場に平行に動く場合は、緩和効果は無視でき、電解質水溶液中(比誘電率εr, 粘度η)における円柱(半径α)の移動度は次のSmoluchowskiの式で与えられる。
 (1)
(1)ここで、εoは真空の誘電率である。円柱が電場に垂直に動く場合、eζ/kT≤4(室温ではζ ≤100mV)ではμ‖は以下の式で与えられる(e=素電荷、k=Boltzmann定数、T=絶対温度)1)。
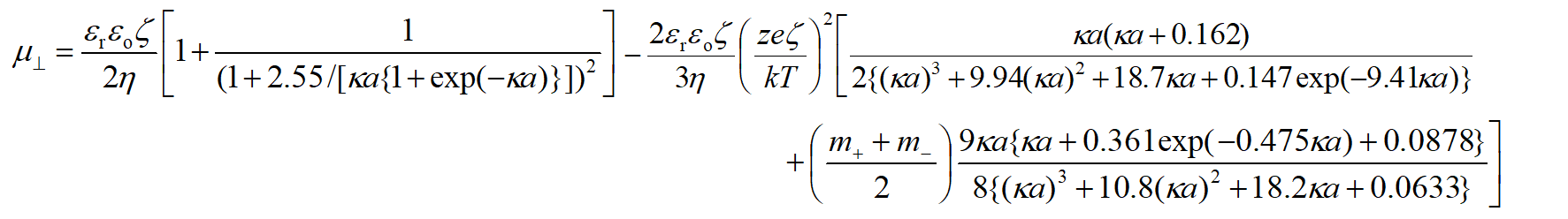 (2)
(2)m±はカチオンとアニオンの無次元抵抗係数で抵抗係数λ±、拡散係数D±、極限等量伝導度$Λ_±^o$と次式で結ばれる。
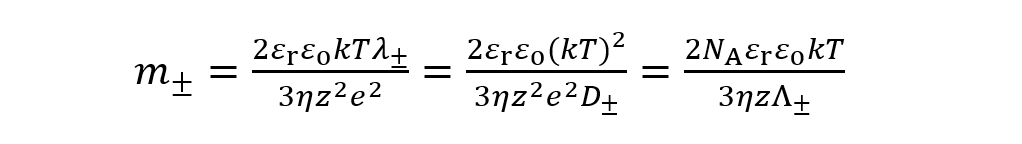 (3)
(3)NA はアボガドロ数である。(2)式右辺の第1項はHenryの式であり(第26回コラム(2)式)、第2項と第3項が緩和効果による補正項である。
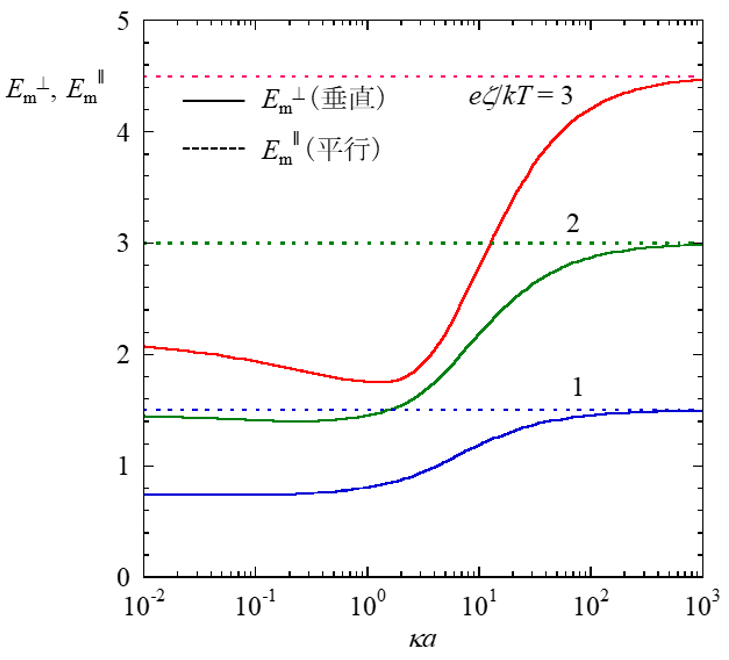
円柱状粒子(半径α)の無次元移動度Em⊥およびEm‖
図2には、KCl水溶液中(25℃)における無次元移動度
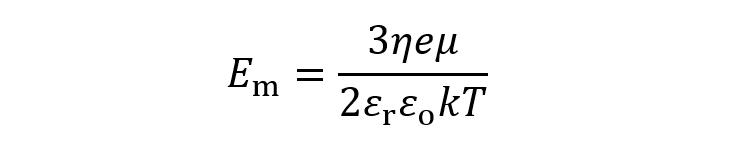 (4)
(4)のκα依存を与えた。Em⊥およびEm‖はそれぞれ円柱が電場に垂直および平行に動く場合の無次元化移動度である。ゼータ電位が低い場合、移動度はHenryの式に帰着する。ゼータ電位が高い場合は、Em⊥に極小が現れる。円柱が電場方向に対して任意の角度で泳動する場合の移動度は以下の平均移動度μavの式で計算される。
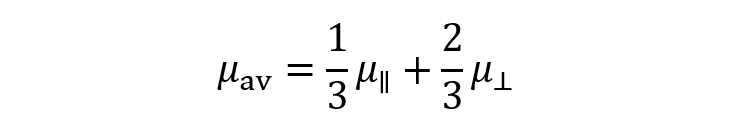 (5)
(5)図3に円柱の平均移動度を等しい半径をもつ球の移動度と比較してある。ゼータ電位が低い場合は両者の差は小さいが、ゼータ電位が高くなると違いが大きくなる。ゼータ電位がさらに高い場合でかつκα ≥ 30の場合の移動度の近似式は球の場合(第42回コラム表1)に一致することが示される2)。
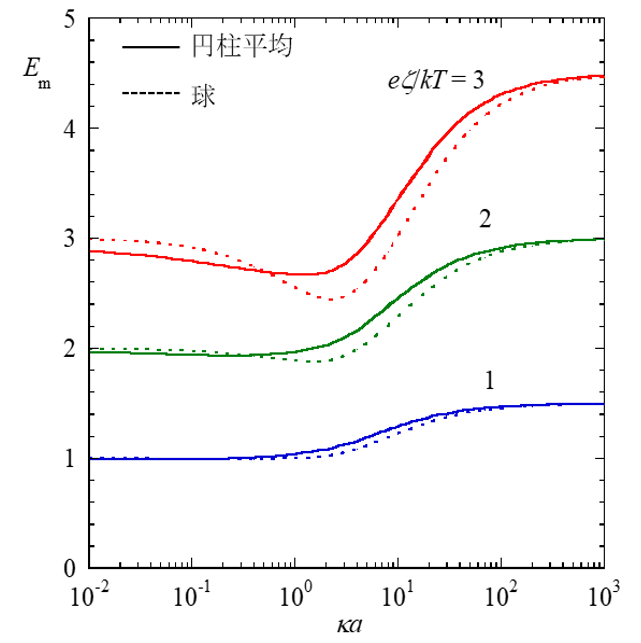
無次元平均移動度Emおよび球状粒子(半径α)の無次元移動度Em
文献
- H. Ohshima, Langmuir, 31, 13633–13638 (2015)
- H. Ohshima, Colloid Polym. Sc., 292, 1227–1233 (2014)

