第39回　球状高分子電解質は柔らかい粒子の特別な場合である

Hermans-藤田の理論（第36回コラム）も平板状とみなせる大きな柔らかい粒子の理論（第37回コラム）もともにBrinkman-Debye-Buecheモデルに基づいている。実際、第37回コラムの(1)式が発表されたとき、Hermans-藤田の式（第36回コラムの(1)式）との類似性が指摘された。多くの場合$λa\gtrsim 1$, $κa\gtrsim 1$, $λd\gtrsim 1$, $κd\gtrsim 1$が満たされるが（α=球状高分電解質の半径，d=表面層の厚さ，1/κ=Debye長，1/λ=Brinkmanの遮蔽長）、この条件下で、電解質水溶液中（η=溶液の粘度）の大きな柔らかい粒子の電気泳動移動度μ（第37回コラムの(1)式）は次式になる。

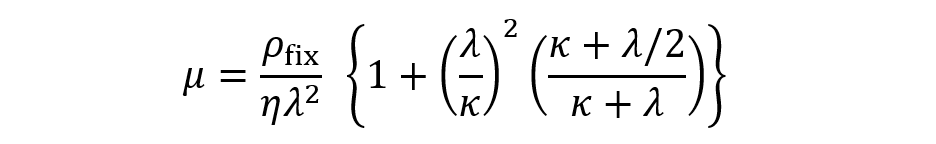(1)

一方、球状高分子電解質に対するHermans-藤田の式（第36回コラムの(1)式）は同じ条件下で次式になる。

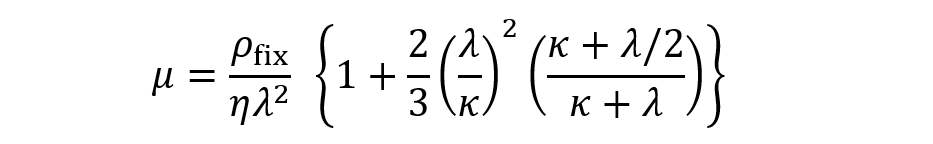(2)

ここで、ρ_fix= 高分子電荷質中の固定電荷密度である。(1)式と(2)式は中括弧内(λ/κ)²の前因子が(1)式では1であるが、(2)式では2/3である。ちょうど、Smoluchowskiの式とHückelの式の違い2/3に類似している。実は、2/3の違いはいずれの場合も本質的に同じ原因すなわち粒子コアによる外部電場の歪みに起因している。実際、この問題を正確に解くと、半径αのコア粒子が厚さdの高分子電解質層に覆われている場合の電気泳動移動度の近似式は次式で与えられる¹⁾。

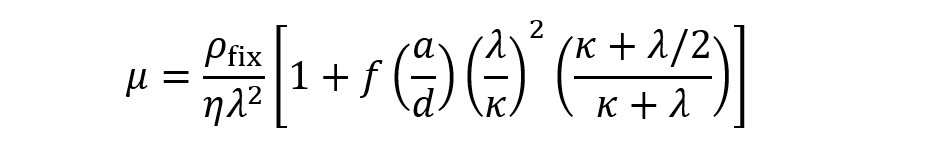(3)

ここで、f(d/α)は外部電場の歪みを表す関数で、次式で与えられる。

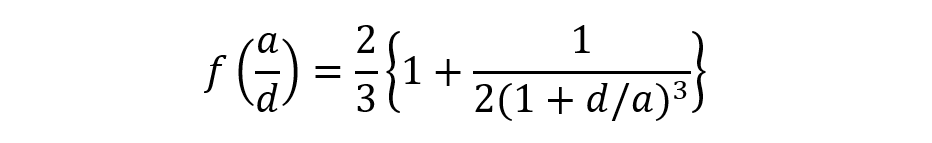(4)

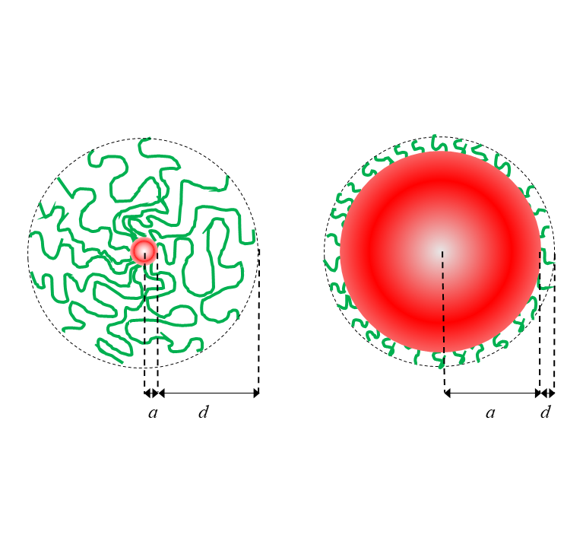図1. 柔らかい粒子の２つの極限(α)さらにα→ 0の極限で粒子コアの無いHermans-藤田の球状高分子電解質になる

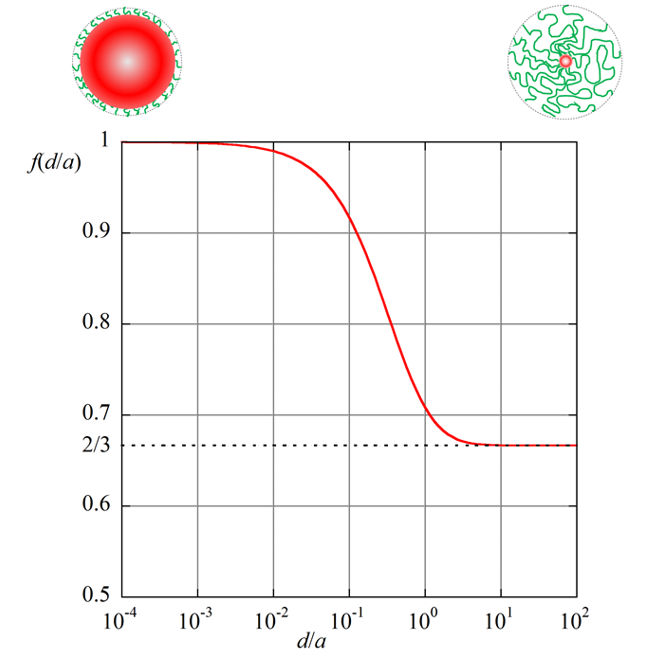図2. 関数f(d/α).α= コア半径 d =高分子電解質層の厚さ

なお、(1)式は電位が低い時の近似式であるが、高電位まで適用可能な式として次式が提出されている。

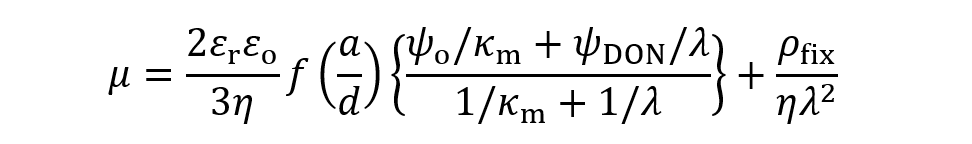(5)

ここで、ψ_o= 高分子電解質層先端の電位、ψ_DON= Donnan電位、1/κ_m=表面電荷層内のDebye長である¹⁾