第23回 Smoluchowskiの式とHückelの式の2/3の違い
Smoluchowskiの式とHückelの式の違いが何に起因するかをみるために、粒子周囲の電場の様子を調べよう。電場Eの中に半径αの球状粒子がある。球の中心に原点Oを置く球座標(r, θ, φ)を定める。外部の任意の場所にける電位Ψは対称性からrとθ のみに依存し、次のように表される。
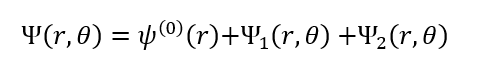 (1)
(1)右辺第1項のψ(0)(r)は電気二重層電位、第2項のΨ1(r, θ)は外部電場および粒子の存在による電場の歪み(電気泳動遅延効果とよぶ)に対応する電位、第3項のΨ2(r, θ)は電気二重層の変形(緩和効果)に対応する電位で粒子のゼータ電位が低いときは無視できる。なお、(1)式では外部電場は電気二重層の電場より弱いと仮定して外部電場Eに比例する項のみが考慮されている(外部電位が大きい場合の電気泳動については後のコラムで述べる)。さらに、Ψ1(r, θ)は以下のように表される。
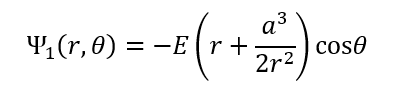 (2)
(2)
(2)式の右辺かっこ内の第1項rは外部電場、第2項r + α3/2r2は粒子の存在による外部電場の歪みに対応する。電解質イオンが粒子内部に侵入できないため、粒子表面で表面に垂直な電場成分がゼロになるように電場の歪みが生じ、電場は粒子表面に平行になる。
図1はΨ1(r, θ)に対応する電場の様子をMathematicaのStreamPlotを用いて作図したものである。図の曲線は電気力線である。力線の向きと密度は電場の向きと強さを表す。電場が粒子表面に平行になるように歪められ、かつ粒子表面近傍で電気力線が押し付けられて互いの間隔が狭くなり、電場が強くなっていることがわかる。
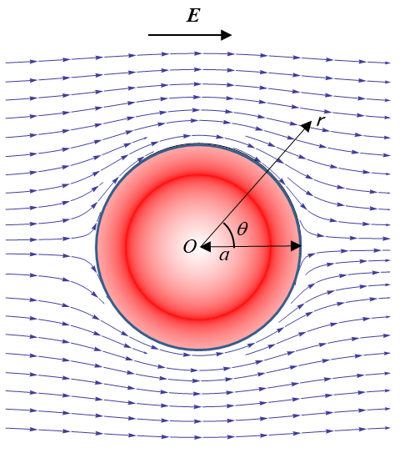
図1. 粒子周囲の電気力線の分布。MathematicaのStreamPlotによる。
元の外部電場と歪み電場は表面近傍でそれぞれr ≈ α, r + α3/2r2 ≈ (3/2)αであるから、電場は表面近傍で3/2倍強くなる。
粒子周囲のイオンの密度分布を電気力線の分布の図1に重ねた結果が図2と図3である。電気二重層が薄い場合(図2)、イオンは粒子表面の3/2倍強められた電場を感じている。これはSmoluchowskiの場合である。一方、電気二重層が厚い場合(図3)、ほとんどのイオンは元の歪められていない電場を感じている。これはHückelの場合である。
この結果、図2の場合(Smoluchouski)の方が図3(Hückel)に比べて、電気泳動移動度が(3/2)倍早くなる(図3の場合の方が(2/3)倍遅くなる)、こうして、Smoluchouskiの式に無かった係数2/3がHückelの式に付くことになる。
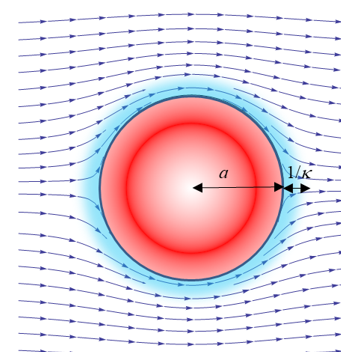
図2. 薄い電気二重層の場合(Smoluchowski)
イオンは粒子表面近くの強く歪められた電場を感じる
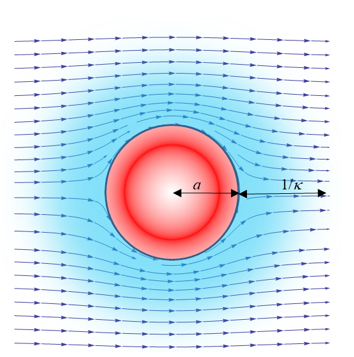
図3. 厚い電気二重層の場合(Hückel)
ほとんどのイオンは元の歪められていない電場を感じる

