第30回 液滴の電気泳動

電場Eのもとで液滴が電気泳動を行うと液滴内部に液体の流れが生じる（図1参照）。このため、固体粒子に比べ電気泳動速度は増大する。球状の水銀粒子内外の流速分布を図2に与えた。

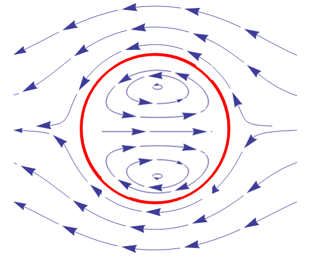
図1. 球状の液滴内外の流線分布
(Mathematica StreamPlotによる)

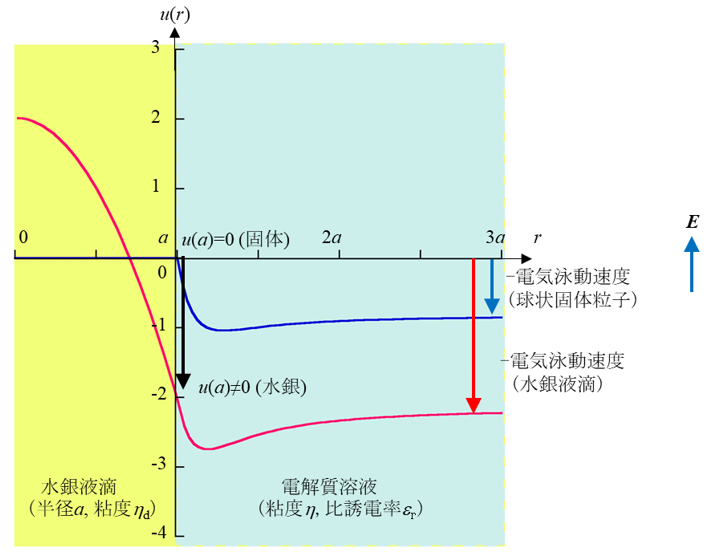
図2. 水銀液滴内外の流速分布u(r)（赤線）および球状固体粒子周囲の電気浸透流速u(r)（青線）

この図でu(r)（赤線）は流速の接線成分（粒子表面に平行な成分）のrに依存する部分を表す。ただし、rは球の中心0から測った距離である。比較のために固体粒子の場合のu(r)も示してある（青線）。r→∞における流速u(-∞)が電気泳動速度Uに負号を付けた量になる。電気泳動速度Uをさらに電場で割った量が電気泳動移動度μ= U/Eである。 液滴の粘度η_d→∞で液滴は固体になり、流速分布u(r)は固体粒子周囲の流速分布u(r)（青線）に帰着する。前回コラムの液体膜の場合のように、液滴内部で液体の流動が起きるために、固体表面の場合と違って、液滴表面上の流速u(0)はゼロにならずに、有限の値をとる。この結果、液滴粒子の電気電気泳動速度は固体粒子の電気泳動速度より大きな値を示す。

液滴の電気泳動移動度μの一般式¹⁾から以下の近似式が導かれる²⁾。この式は液滴に対するHenryの式に対応する。

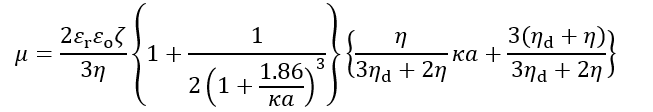　(1)

この式をみると、κα→∞の極限で次式になり、前回コラムの(1)式と一致しない。球状固体粒子の場合は、κα→∞の極限でSmoluchowskiの式に帰着したが、液滴の場合はそうはならない。これは、液滴の特徴であり、κα→∞で μ→∞になる。

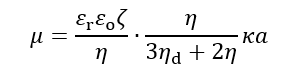　(2)

• 《文献》
• 1) H. Ohshima, T.W. Healy, L.R. White, Electrokinetic phenomena in a dilute suspension of charged mercury drops. J. Chem. Soc. Faraday Trans. II., 80, 1643-1667 (1984).
• 2) H. Ohshima, A simple expression for the electrophoretic mobility of charged mercury drops. J. Colloid Interface Sci., 189, 376-378 (1997).