第21回 Smoluchowskiの式の厳密な導出：Navier-Stokesの式

電場Eの下で速度Uで泳動する粒子（表面は平板とみなせる）の電気泳動移動度 μ= U/Eに対するSmoluchowskiの式をNavier-Stokesの式から厳密に導く。平板表面に垂直にx軸をとり、原点を平板表面に定める（図1）。位置xとx + Δxに挟まれた厚さΔxの薄い液体の層に働く力のつり合いを考えよう。この液相には電場からの力と粘性力が働く。液体中に速度の異なる（速度勾配のある）部分があると速度差をなくそうとする力が生じる。これが粘性力であり（液体の粘度）×(速度勾配) = ηdu/dxで与えられる。xの面では液層の内側に比べて外側の方が遅いので液層に対して図の上向きに力が働く。x＋Δxの面では逆に外側の方が早いので液層に対して図の下向きに力が働く。したがって、正味の粘性力（図の上向き）は上記の２つの力の差 ηdu/dx|_x+Δx - ηdu/dx|_xになる。
近似式 f(x+Δx)= f(x)+df/dx・Δxを用いると、正味の粘性力は ηdu/dx|_x+Δx - ηdu/dx|_x = ηd²u/dx²Δxになる。

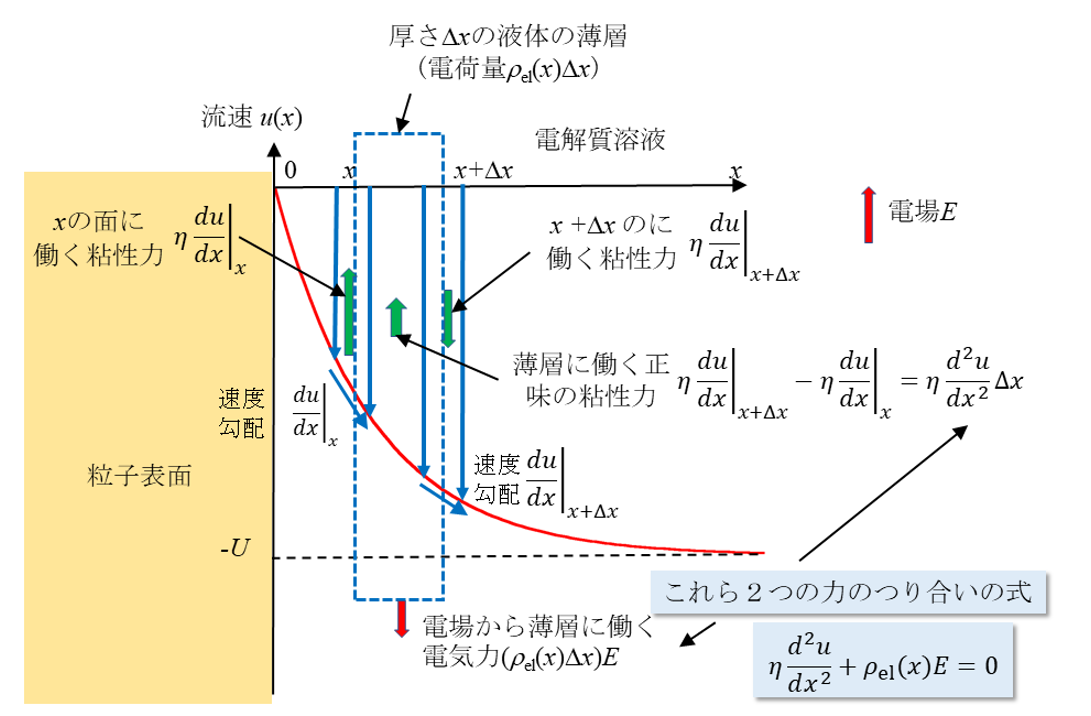
図1. 液体の薄層(厚さΔx)に働く粘性力と電気力のつりあい

一方、この液層に働く電気力は液層に含まれる単位面積当たりの電気量ρ_el(x)Δxに電場E を掛けた量 ρ_el(x)ΔxEで与えられる。ρ_el(x)は位置xにおける電解質イオンによる電荷密度である。たとえば、KCl溶液であれば、xにおけるK⁺イオン由来の電荷量とCl^-イオン由来の電荷量の和である。帯電平板から遠く離れた場所では、電気的に中性でρ_el(x)=0であるが、平板近傍では対イオン（平板の電荷と逆符号のイオン）の方が副イオン（平板の電荷と同符号のイオン）よりも高濃度のため、ρ_el(x)≠0になる。以上より、液層に働く粘性力と電気力のつり合いの式は

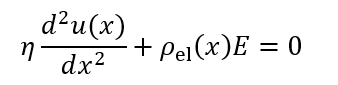(1)

になる。この式は遅い流れに対するNavier-Stokesの式である。ρ_el(x)はさらに位置xにおける電位ψ(x)の2階の導関数とPoissonの式: d²ψ(x)/dx² = -ρ_el(x)/ε_rε_oで結ばれる。この式を(1)式に代入すると次式が得られる。

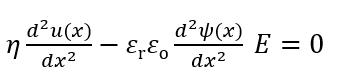(2)

平板表面x= 0ですべりなし条件u(0)=0　および　ψ(x)=ξ、u(∞)=-U、ψ(∞)=0の境界条件の下で、(2)式を解くと、直ちに電気泳動移動度μに対するSmoluchowskiの式が得られる。

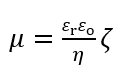(3)