第2回 コロイド粒子間のvan der Waals引力―Hamaker定数(凝集促進因子)
中心間距離rの2分子間にはvan der Waals引力が働き、そのポテンシャルエネルギーは-C/r6で与えられる。CはLondon-van der Waals定数と呼ばれる。このエネルギーは1/r6に比例するため短距離にしか及ばないが、加算性がよく成り立つため、多数の分子から成るコロイド粒子間には長距離に及ぶ大きなvan der Waals引力が働く。例として、距離hにある分子1と線状高分子2(分子密度N)を考える(図1)。高分子中の幅⊿xの微小部分に含まれる分子の総数はN⊿xである。これらの分子と分子1のvan der Waals相互作用エネルギーは(-C/r6) N⊿xである。したがって、分子1と線状の高分子2の相互作用エネルギーV(h)はx = h からx = ∞までのすべての微小部分からの寄与の合計で表される。
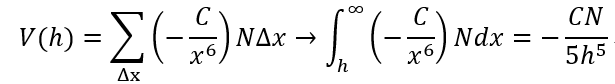
ここで、∑Δx→∫dxの関係を用いた。このように、もともと1/r6に比例する分子間相互作用が線状高分子と1個の分子では1/h5のように短距離性が減少することが示された。
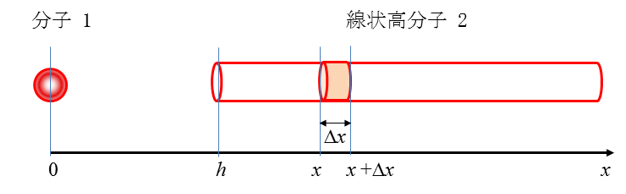
図1 分子と線状高分子
同様の計算をおこない、表面間距離がhまたはHにある種々の物体1(分子密度N1)と2(分子密度N2)のvan der Waals相互作用エネルギーVの表式を図2にまとめた。球状粒子間では1/Hに比例する長距離相互作用になることがわかる。ここで、登場する定数A = π2C12N1N2はHamaker定数とよばれる。ただしC12は物体1の分子と物体2の分子間相互作用に対するLondon-van der Waals定数である。Hamaker定数Aは物体間の相互作用エネルギーの大きさを特徴づけるパラメタである。Aが大きいほどコロイド分散系は強く凝集するので、Aは凝集促進因子とよばれる。
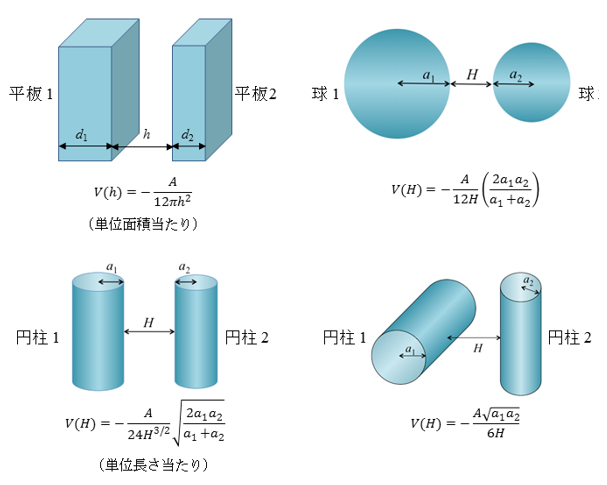
図2 種々の形状のコロイド間のvan der Waals相互作用エネルギー
(H またはhは物体のサイズより十分小さいとする)
(H またはhは物体のサイズより十分小さいとする)

