第31回 金属粒子の電気泳動

ここまでのコラムではコロイド粒子の電気泳動を考える際に、粒子が絶縁体か金属か区別しなかった。その理由は、Overbeek-O’Brien-Whiteによる電気泳動の標準理論では、ゼータ電位が同じならば絶縁体と金属は同一の電気泳動移動度を示すからである。しかし、この標準理論の基礎の一つであるHenryの理論¹⁾では絶縁体と金属では異なる結果が導かれている。電解質溶液中（電気伝導度σ，比誘電率ε_r，粘度η，Debye-Hückelのパラメタκ）を電気伝導度σ_pの球状粒子（半径α，ゼータ電位ζ）が電気泳動するとき、電気泳動移動度μをμ= (ε_rε_oζ/η)f(κα)とおいて、Henry関数f(κα)を定義する。Henry理論によると、Henry関数f(κα)は図1のように比σ_p/σに依存する。一番上曲線（σ_p/σ= 0）が絶縁体粒子に対応し、通常のHenry関数を表す。一番下の曲線（σ_p/σ= ∞）が金属に対応する。καの小さい場合（電解質濃度が低く電気二重層が厚い場合）は、f(κα)のσ_p依存性は小さいが、καの大きい場合（電解質濃度が高く電気二重層が薄い場合）は金属と絶縁体では違いが大きい。とくに、金属の場合、κα→∞ではf(κα) →0，すなわち、動かなくなる。絶縁体の場合にSmoluchowskiの式（f(κα) →1）になるのと大きく異なる。しかし、この結果に強く反論したのがOverbeek²⁾である。もし、Henryの考えた通りならば、図2に示すような反応が粒子表面で生じることになる。つまり電解質溶液中では電流の担い手は電解質イオンであるのに対し、金属内部では電子が電流を担う。その結果、この過程は電解質イオンの粒子表面における中和反応（イオン→原子）と反対側の表面における金属原子のイオン化反応（原子→イオン）を伴う。このようなことは通常の電気泳動実験のもとでは、印加電圧が低くて起こらないというのがOverbeekの指摘であり、現在の標準理論もこれを採用して、「電解質イオンの流れは粒子表面を通過しない」という境界条件を基にしている。この結果、絶縁体と金属は同じHenry関数に従う結果になる。ただし、印加電圧が高い場合はこのような化学反応が起きる可能性は否定できない。ちょうど、電池における電極における化学反応の対応するが、今後の問題である。

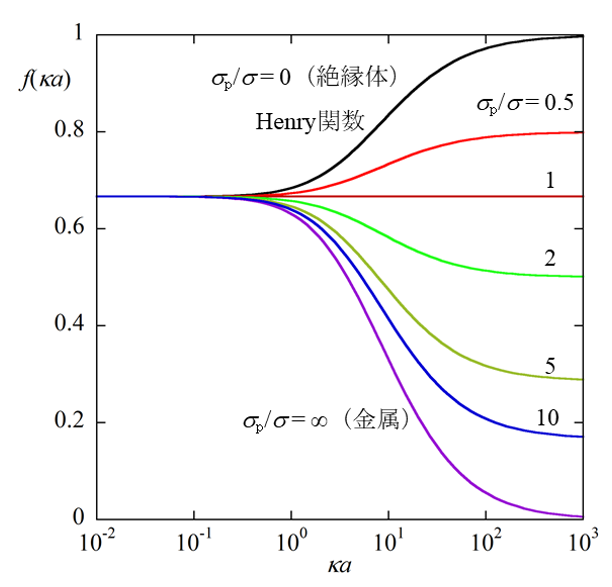図1. 球状粒子のHenry関数f(κα)と電気伝導度σp 絶縁体の場合が通常のHenry関数1).電気泳動の標準理論では、f(κα)のσp依存は否定されている2). 金属でも絶縁体のHenry関数が適応できる

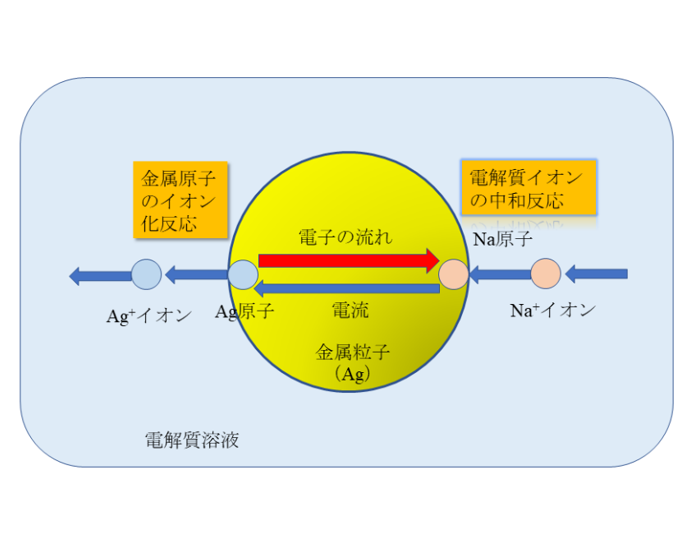図2. Henryの考えた金属粒子表面の化学反応 電気泳動の標準理論では、このような化学反応は起きないとされている

文献

1. D.C. Henry, The cataphoresis of suspended particles. Part I. The equation of cataphoresis. Proc Roy Soc London Ser A 133: 106-129 (1931).
2. J.Th.G. Overbeek and P.H. Wiersema, The Interpretation of Electrophoretic Mobilities. In M. Bier (ed) Electrophoresis: Theory, Methods, and Applications