第44回 ゼータ電位から見かけの表面電位を求め粒子間静電相互作用エネルギーを計算する
ζからψeffを求めVel(H) を計算する手順
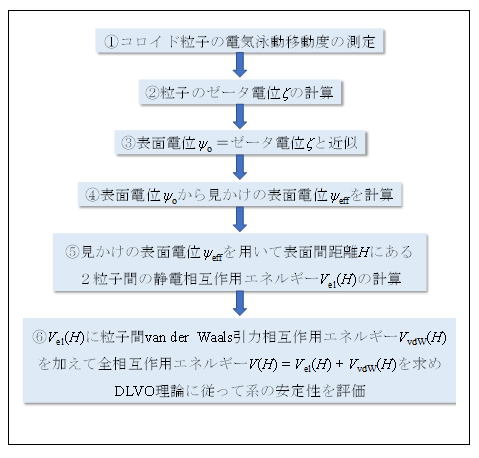
粒子の電気泳動移動度の測定から粒子のゼータ電位を求め、見かけの表面電位が得られると、以下のように2個の粒子間静電相互作用エネルギーが計算されDLVO理論に基づいて微粒子分散系の安定性を議論できる。
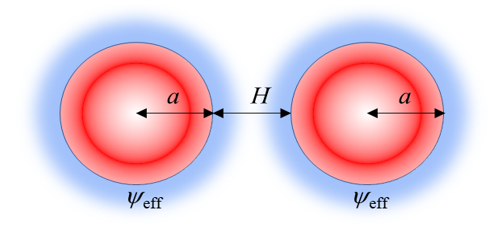
図1. 2個の球間の静電相互作用
図1のように対称型電解質水溶液中(価数z, バルク濃度n, Debye-Hückelパラメタκ)において表面間距離H にある2個の等価な球状粒子間(半径α, 表面電位ψo)の静電相互作用エネルギーVel(H)は次式で与えられる(第6回コラム(2)式)。
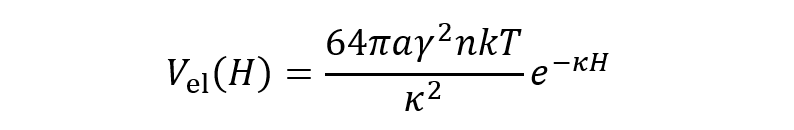 (1)
(1)ここで、γ=tanh(zeψo/4kT)であり、粒子の見かけの表面電位とψeff= (4kT/ze)γで結ばれる(k= Boltzmann定数,T= 絶対温度,e= 素電荷)。(1)式を次式のように書き換えると、対象型電解質以外の一般の電解質溶液中における静電相互作用に適用できる一般式が得られる。
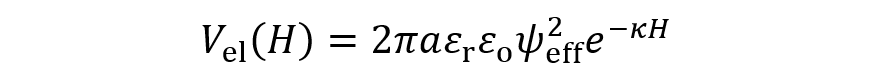 (2)
(2)代表的な電解質に対するDebye- Hückelパラメタκと見かけの表面電位ψeffを表1にまとめた。これらはいずれも電解質の型と濃度に依存する。ここで、εr= 媒質の比誘電率,εo= 真空の誘電率、κ= Debye-Hückelのパラメタであり、κの逆数1/κはDebye長すなわち粒子周囲の拡散電気二重層の厚さである。表1の電解質濃度nの単位はm-3で、M単位で表した濃度C (M)へ変換するには、n= 1000NACの関係を用いればよい。(NA=アボガドロ数)。低電位は、いずれの場合もψeffは真の表面電位ψoに帰着する。
表1 Debye-Hückelのパラメタκおよび見かけの表面電位ψeff


