第27回 Henryの式と粒子の表面電荷密度:円柱の場合
球の場合(第25回)と同様に、円柱状粒子の場合について、電気泳動移動度をゼータ電位ζのかわりに表面電荷密度σを用いて書き換えようとすると円柱に特有のある問題が生じる。液体媒質 (比誘電率εr, 粘度η, Debye長1/κ) 中にある円柱状粒子(半径α)の周囲の電位分布ψ(r)および表面電位ψoと表面電荷密度σ の関係はψoが低い場合は次式で与えられる。
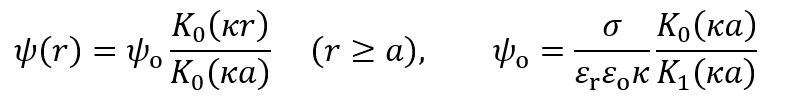 (1)
(1)
ここで、K0(κα)とK1(κα)はそれぞれ0次と1次の変形ベッセル関数である。電気二重層(厚さ1/κ)が円柱の半径αに比べて十分に薄い場合(κα»1)、 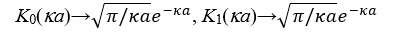 であるから、ψoとσの関係はψo= σ/εrεoκになり平板の場合に一致するので予想通りの結果になり問題はない。
半径αの球の場合も、κα»1のとき、ψo= σ/εrεoκになる(第4回コラムの(1)式参照)。ところが、逆に電気二重層が円柱の半径に比べて十分に厚い場合(κα«1)は、K0(κα)/καK1(κα) → log(1/κα)であるから、
であるから、ψoとσの関係はψo= σ/εrεoκになり平板の場合に一致するので予想通りの結果になり問題はない。
半径αの球の場合も、κα»1のとき、ψo= σ/εrεoκになる(第4回コラムの(1)式参照)。ところが、逆に電気二重層が円柱の半径に比べて十分に厚い場合(κα«1)は、K0(κα)/καK1(κα) → log(1/κα)であるから、
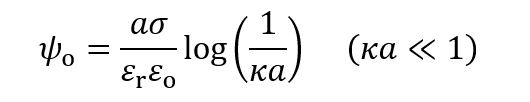 (2)
(2)が得られる。つまり、κα→0でψoは無限大になってしまう。球の場合、κα→0でψo= σα/εrεo=Q/4πεrεoα (Q=4πασ2は表面電荷の総量)で有限であり、円柱と球で結果が大きく異なる。この違いは、κα→0で球の場合はψ(r)= σα2/εrεor= Q/4πεrεor(クーロン電位)となって1/rに比例するが、 円柱の場合のクーロン電位は(σα/εrεo)log(1/κr)となり、対数が登場するためである。これは円柱の特徴である(図1)。

図1. 円柱の表面電位のκα 依存.
ここで、ψo*=ψo/(ασ/εrεo)
同様の問題(κα→0で無限大)が、円柱状粒子が円柱の軸に垂直に運動する場合に円柱が受ける粘性抵抗(Stokes抵抗)および電気泳動移動度μ⊥についても起きる。第22回コラムで述べたように、電場Eのもとで、粘度ηの液体媒質中を速度Uで動く半径αの球の場合、κα→0における電気泳動移動度μ(Hückelの式)が球に働く電気力QEとStokes抵抗6πηαUのつりあいから求められた。この方法を円柱に適用しよう。 単位長さあたりの円柱に働く電気力はQE=2πασE(Q=円柱の単位長さあたりの表面電荷の総量=円柱の周の長さ2παと表面電荷密度σの積)である。ところが、Stokes抵抗は4πηαU/log(1/κα)となって、κα→0で無限大になる。したがって、つりあいの式はμ⊥= U/E(U, EはそれぞれU, Eの大きさ)を計算すると、以下の(3)式が得られ、μ⊥もκα→0で無限大になってしまう。
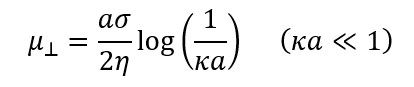 (3)
(3)しかし、(2)式で与えられる円柱の表面電位ψoを円柱のゼータ電位ζとみなし、(3)式に登場するσをζで置き換えると、次式が得られる。
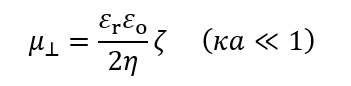 (4)
(4)(3)式も(4)式もどちらもκα→0における円柱に対するHückelの式である。 しかし、σで表した(3)式はκα→0で無限大になるが、ζで表した(4)式では、見かけ上、この困難が回避され、(4)式はκα→0で無限大にならず有限である。Henryの式は正しくκα→0で(4)式を与える。 このように、μ⊥に対するHenryの式においてζをσで置き換えて第25回コラムのような図を描くと図の左端で無限大になってしまうので、今回はそのような図を描くことはしない。円柱状粒子の電荷を求めるときは、円柱に対するHenryの式(第26回コラム)用いて電気泳動移動度の実測値からζを計算し、(1)式の第2式を用いて、σを計算する。

