第45回 固体表面の表面電位は電位が高くなると表面電荷密度に比例しない
電位が低い場合は、粒子表面近傍における電位は指数関数的に減衰し、粒子の表面電位ψoは表面電荷密度σに比例する。固体表面の曲率がDebye長1/κより十分大きく固体表面を平面と見なせる場合、粒子表面近傍における電位分布ψ(x)はψ(x)= ψoexp(-κx) およびψoとσの関係は ψo= σ / εrεoκで表される(第5回コラム(1)式で平板の場合参照)。ここで、εr =媒質の比誘電率、εo=真空の誘電率、κ =Debye-Hückelのパラメタである。κの表現は電解質の型によって異なる(第44回コラム表2)。電位が高い場合、ψoとσは比例しない。代表的な電解質の型に対して、厳密にPoisson-Boltzmannの式を解いて得られる電位分布ψ(x)とψoとσの関係式を表1と表2に与えた。さらに図1には1価対称型電解質水溶液中(25℃)においていくつかの電解質濃度C (M)におけるψoとσの関係を示した。実線が厳密解(表1参照)、点線が近似解(ψo= σ / εrεoκ)である。電位が高くなると(50 mV以上)、ψoとσの直線関係が成立しないことがわかる。
表1 電位分布ψ(x)

表2 表面電位ψoと表面電荷密度σの関係

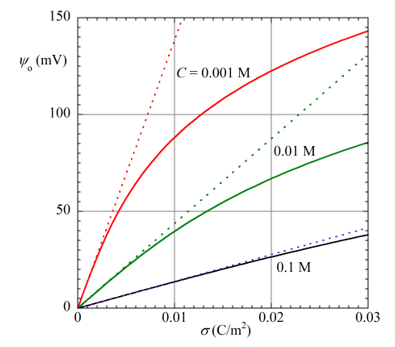
図2. 1価対称型電解質水溶液中における平板上粒子のψoとσの関係(25℃)
3つの電解質濃度C=0.1, 0.01, 0.001Mで計算。
実線:厳密解(表2のz:z型電解質でz=1の場合)
点線:近似解ψo= σ / εrεoκ
表面電位ψo≤ 50mVでは近似解で十分であることがわかる。
3つの電解質濃度C=0.1, 0.01, 0.001Mで計算。
実線:厳密解(表2のz:z型電解質でz=1の場合)
点線:近似解ψo= σ / εrεoκ
表面電位ψo≤ 50mVでは近似解で十分であることがわかる。

