第40回 ゼータ電位が高くなると、電気泳動移動度からゼータ電位が計算できない?
DLVO理論の実験的証明で名高い筑波大学の古澤邦夫教授がオランダ留学中の経験談である。1971年12月開催のあるミーティングでOverbeek教授の弟子であるWiersema氏が「粒子のゼータ電位が100mV以上あると、電気泳動移動度からゼータ電位を求めることは不可能である」と興奮気味に語ったそうである(古澤邦夫著「フラットランドから出発」)。これまで述べてきたように、コロイド粒子の電気泳動移動度は粒子のゼータ電位に比例する。これは、Smoluchowski、Hückel、Henryの電気泳動理論においては、ゼータ電位が低い場合が扱われているからであり、その結果は1価対称型電解質の場合、50 mV以下で良い近似とされる。
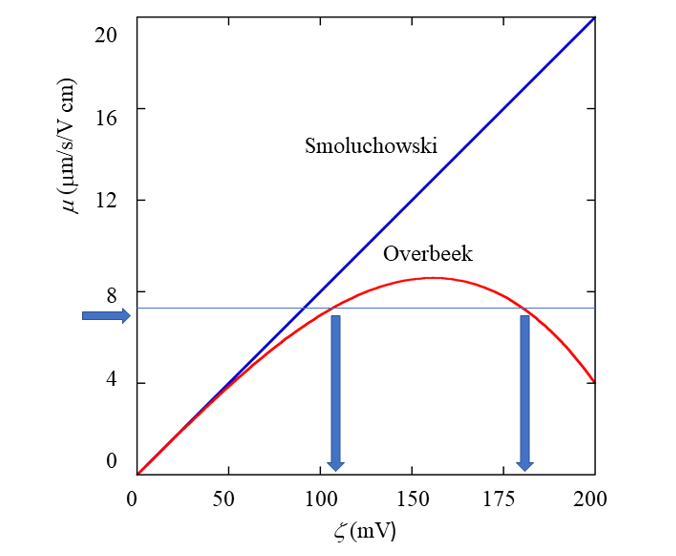
図1. 電気泳動移動度μとゼータ電位ζ
ゼータ電位が高い場合の計算はOverbeekの学位論文によって行われた。Overbeek は電気泳動移動度μをゼータ電位ζのべき級数の形に表して、ζ3の項まで求めることに成功した。Overbeekの理論からは、ζの低いときはSmoluchowskiの式のようにμはζに比例して増大するが、ζが高くなるとζ3の項の存在のために、μの増加が抑えられることが示される。さらにζが高いと、極大を過ぎるとμはζとともに減少する場合がある。つまり、電気泳動移動度に極大が存在することになる。この極大はたまたまOverbeekの用いた近似の範囲内で生じた結果なのであろうか。さらに近似を進めてζの高次の項が得られても極大が相変わらず存在するのか、それとも極大が消失しμはζとともに単調に増大し続けるのか。この問題は、長い間、論争の的であった。もし、図1のように極大が存在すると、μからζを求める場合、Smoluchowskiの式では、一つの電気泳動移動度の値に一つのゼータ電位が対応するので問題はないは、一方、Overbeekの理論では、電気泳動移動度の実測値に2つのゼータ電位が対応し、どちらを採用するか困ることになる。
この間の論争の様子を図2に示す。1966年には、前述のWiersemaおよびLoeb、Overbeekが渡米しIBMのコンピュータで計算したが、計算の収束が悪く極大の存在の確認までには至らなかった。極大の存在を予測した論文が発表された後に同じ著者によってそれを否定する論文が発表されたこともあった。極大の存在がはっきりしたのは、1978年のO’BrienとWhiteによる数値計算の結果である。その後、極大の存在が解析的にも確認された。こうして古澤先生に語ったのWiersemaの心配は確定的になった。ただし、現実問題としては、図1のゼータ電位の2つの候補のうち、高電位の方は採用せず(それほど高いゼータ電位をもつ粒子の存在は考えにくいので)、低電位の方を選ぶことが一般的である。
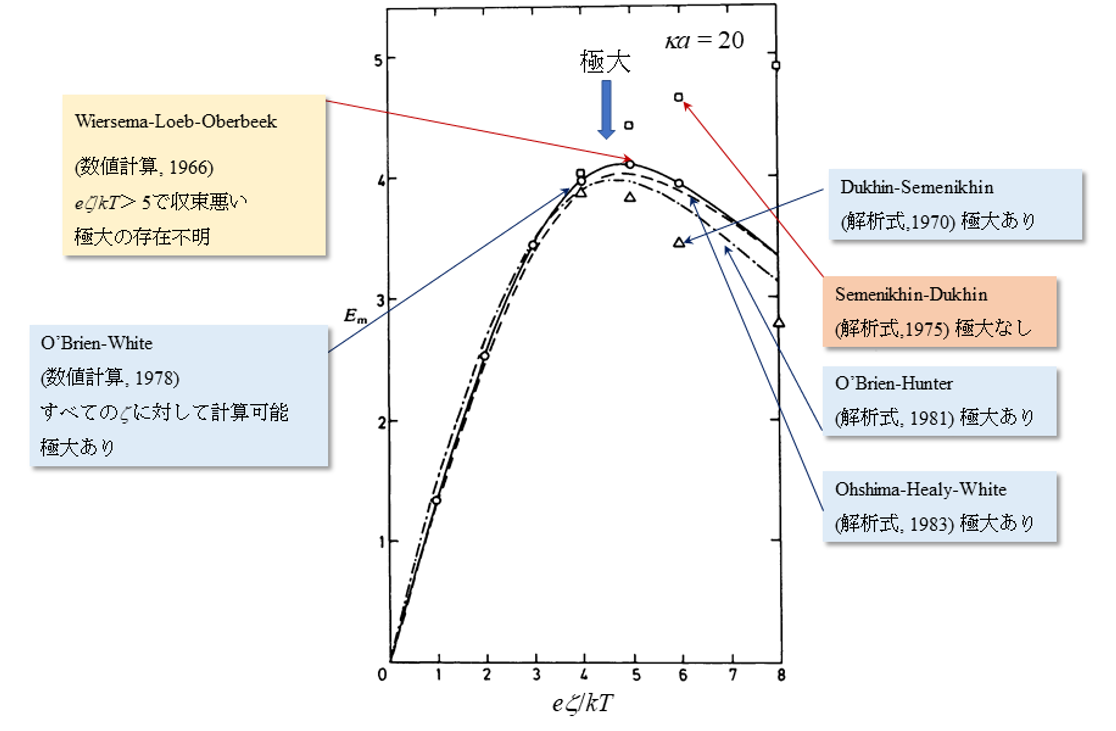
図2. 電気泳動移動度の極大をめぐる論争 Em=無次元化した電気泳動移動度,
eζ/kT = 無次元化したゼータ電位(e=素電荷,k=Boltzmann定数,T=絶対温度)
κα=20 (κ=Debye-Hückelパラメタ,α=粒子の半径)

