第49回 コロイド振動電位(CVP)
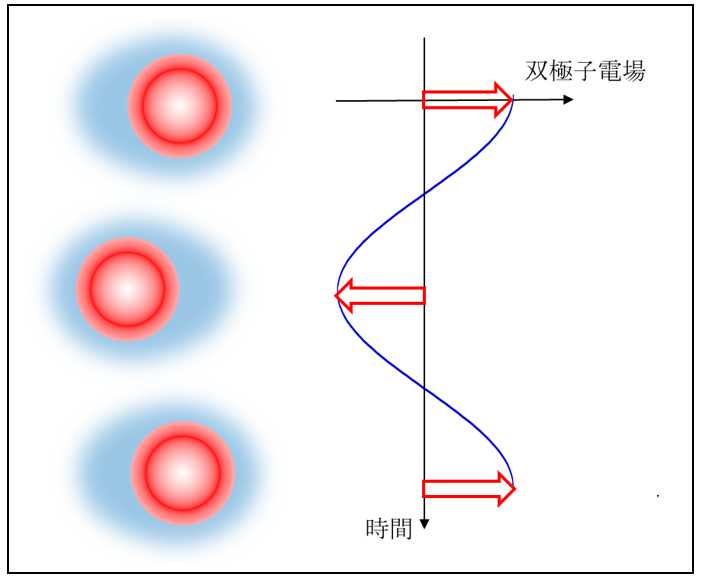
前回のコラムで述べた沈降電位は重力の下で帯電粒子が沈降するときに発生する電位であったが、コロイド粒子を分散させた電解質溶液に超音波を照射すると同様な電位が発生する。この電位はコロイド振動電位(Colloid Vibration Potential略してCVP)と呼ばれる。超音波により粒子が振動するが、粒子周囲の電気二重層中のイオンが粒子の振動に追従できず、電気二重層が変形する。この結果、双極子電場ができる。各粒子からの電場が重なって巨視的な電場が生じる。これがコロイド振動電場であり、異なる2点間の電位差(コロイド振動電位CVP)として観測される。CVPの発生は沈降電位に類似した界面電気現象であり、沈降電位における重力の役割を超音波照射によって生じる圧力勾配が担う。
CVPの式は沈降電位の式(第48回コラムの(4)式)において、重力加速度gを圧力勾配に比例する因子∇p/ρoで置き換えると次式のように得られる。
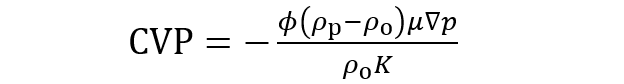 (1)
(1)ここで、μ=粒子の電気泳動移動度、φ=粒子の体積分率、∇p=超音波照射による圧力勾配、ρp=粒子の質量密度、ρo=媒質の質量密度、K=溶液の電気伝導度である。沈降電位と同様、異なる界面動電現象である電気泳動移動度μとCVPが比例するが、これもOnsagerの相反定理の一例である。なお、(1)式に登場するμは厳密には振動数に依存する動的電気泳動移動度であるが、近似的には静電場における通常の電気泳動移動度で置き換えられる。 (1)式は粒子の体積分率φの小さい希薄系を対象に導かれた式である。濃厚系まで適用可能な任意のφに適用できるCVPの式として次式が導かれている。
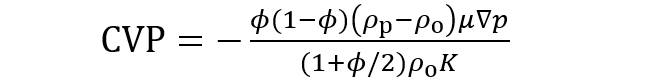 (2)
(2)(2)式右辺の因子(1-φ)/(1+φ/2)が濃厚系の効果を表す。図2にこの因子をφの関数として示した。φが1%未満なら(1-φ)/(1+φ/2)を1と近似でき、(2)式は(1)式に帰着する。言い換えれば、濃厚系の効果はφが1%以上になると顕著になる。なお、(2)式のμは厳密にはφに依存する濃厚系の電気泳動移動度(第46回コラム)であるが、近似的には静電場における通常の電気泳動移動度で置き換えられる。