第48回　沈降電位

重力の下で帯電コロイド粒子が沈降すると沈降電位と呼ばれる電位が発生する（図1）。重い粒子の沈降に軽い電気二重層中のイオンが追い付けず、電気二重層が変形する。この結果、電気双極子が発生し電場ができる（図2）。各粒子から生じる電場はミクロな電場であるが、それぞれの電場が互いに重なって巨視的な大きな電場になる。これが沈降電場である。実験的には、異なる2点間の電位差（沈降電位）として観測される。

図1. 重力の下で帯電したコロイド粒子が沈降する

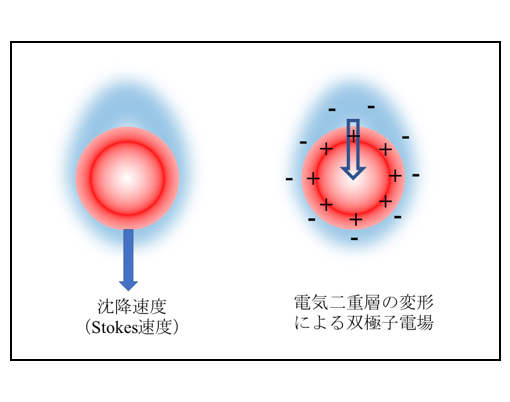図2. 沈降する帯電粒子から生じる双極子電場

半径αの球状粒子が速度Uで沈降する場合、粒子に働く重力(4π/3)α³ρ_pgと浮力(4π/3)α³ρ_ogおよびStokesの粘性抵抗6πηαUがつりあい、定常状態に達すると、Uは次式で与えられるStokes速度U_STに等しくなる。

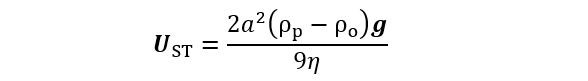　(1)

ここで、g=重力加速度、ρ_p=粒子の質量密度、ρ_o=媒質の質量密度、η=媒質の粘度である。帯電粒子が沈降すると電荷が移動することになるので、電流Iが発生する。ただし、粒子のもつ電荷qのみが移動するのではなく同時に電気二重層も移動するので、この寄与も加えた粒子の持つ実効電荷q_effを導入する（後に(3)式で定義）。単位体積当たりの粒子数をnとすると、Iは次式で与えられる。

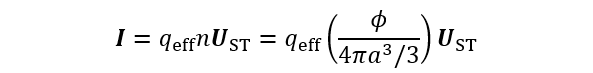　(2)

ここで、φ=(4π/3)α³nは粒子の体積分率である。しかし、電気泳動と違い、コロイド粒子分散系に対して電流Iを保持する外部電源が接続されていないので、分散系内部にIを打ち消すような電場が発生する。この電場が沈降電場E_SEDである。E_SEDによる電流をI_SEDとすると、オームの法則によって、I_SED=KE_SEDになる。ここで、Kは系の電気伝導度である。I_SEDはIを打ち消さなければならないので、I_SED+I=0が成り立つ。さて、粒子の実効電荷q_effは粒子の電気泳動移動度μと以下の関係がある。

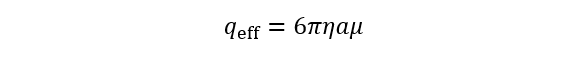　(3)

この式は電場E中で、速度Uで半径αの粒子が泳動するとき、粒子に働く電気力q_effEとStokesの粘性抵抗6πηαUのつりあいq_effE=6πηαUからμ=U/E（U，EはU，Eの大きさ）と置いて求められる。 以上の諸式から沈降電場に対する式が得らえる。

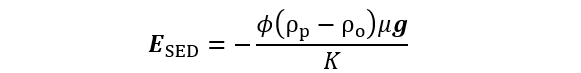　(4)

ただし、右辺の負号はIとI_SEDが逆向きであることを示す。このように、重力場における沈降電場と電場における電気泳動移動度が互いに比例する結果が得られたが、これはOnsagerの相反定理とよばれる定理の一例である。