第28回 液滴に働くStokes抵抗：液滴と固体粒子の違い

これまで、球状および円柱状の固体粒子の電気泳動を扱ってきたが、水銀や水中の油滴（エマルション）のような液滴の場合はどうなるであろうか。固体と違って液滴内部で流体の流れが生じる点で液滴の電気泳動は固体粒子の電気泳動と大きく異なる。図１は第23回コラムにおいて外部電場中の粒子周囲の電場（電気力線）の様子を示すために用いたMathematicaのStreamPlotにより作図した球状粒子内部の流線分布である。 球内部の粘度が大きいと固体球に近づき粒子内部の流れは消失する。固体粒子の場合、粒子周囲を流れる液体の速度（粒子に対する相対速度）は粒子表面でゼロになる（第19回コラムで述べたように、実はこれはあくまで仮定であり、水中を泳動する親水性粒子の場合にのみ厳密に正しい。疎水性粒子の場合は粒子表面と周囲の水分子の引力が弱いため「流体のすべり」が生じる。この問題は後に改めて述べる）。固体粒子と違って、液滴の場合、液滴内部に流動が起きるため、粒子表面で液体の速度はゼロにならない。この結果、液体から受ける粘性抵抗（Stokes抵抗）は固体粒子に比べ小さくなり、粒子は速く動くことになる。

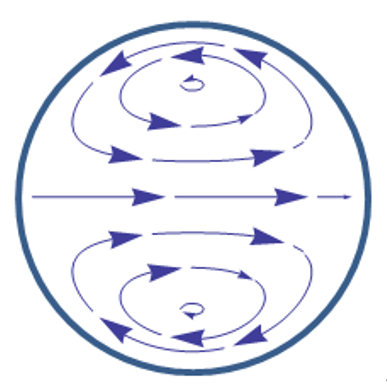
図1. 球状粒子内部の流線分布
(Mathematica StreamPlotによる)

液体媒質（粘度η）中を速度Uで泳動する球状固体粒子（半径α）に働くStokes抵抗は6πηaUであるが、球状液滴（半径α,粘度η_d）の場合、Stokes抵抗は次式で与えられる。

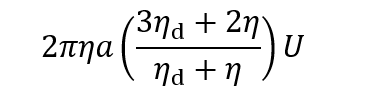　(1)

図2にStokes抵抗のη_d依存を示した。液滴の粘度が無限大（η_d →∞）になると液滴は固体球に近づきStokes抵抗は6πηαUになる。逆に、η_d→0で液滴は気泡に近づきStokes抵抗は4πηαUになる。液滴の粘度が媒質の粘度に等しいときは（η_d =η）、Stokes抵抗は固体と気泡の中間の値5πηαUになる。

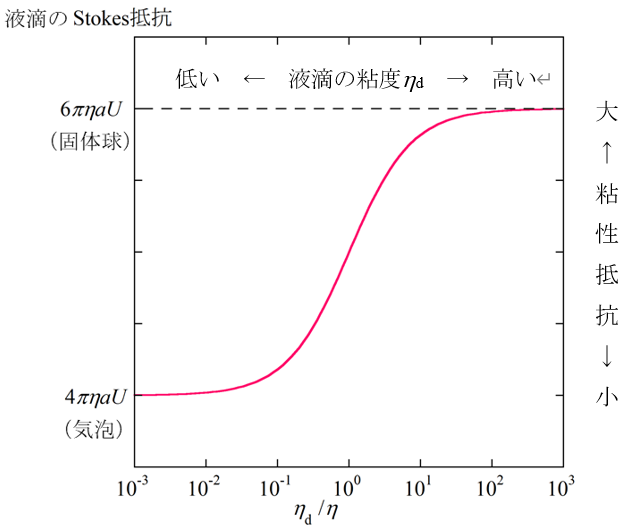
図2. 液滴に働くStokes抵抗

ここで、２つの注意点がある。一つは液滴の形状が球状に保たれるかどうかという問題である。液滴の表面張力が十分大きい場合は、液滴が球状に保たれるとする仮定は妥当である。もう一つの問題点は液滴表面への吸着物質の存在である。エマルションの場合は多くの場合、界面活性剤分子が吸着している。吸着が十分に起こり、表面全体が吸着分子に覆われる場合は、液滴外部の流動が内部に伝わらず、液滴に働くStokes抵抗は固体粒子の場合と同じになる。気泡の表面も何らかの分子が表面に吸着している場合が多い。この場合は気泡の挙動は固体粒子に近く、Stokes抵抗は固体粒子の場合と同じになる。液滴表面への吸着が中程度の場合、吸着平衡を考慮した扱いが必要になるが、難しい問題である。